Homework #11

You can also get the PDF format of Wenqiang’s Homework.

Load data

data165 = read.table("./data/ex16-5.TXT", header = T)

Problem 16.5 (b)

library(ggplot2)
lm.fit = lm(RISK~NOCIG, data=data165)
coefEst = coef(lm.fit)
ggplot(data165, aes(x=NOCIG, y=RISK)) + 
  geom_point() +
  geom_abline(intercept = coefEst[1], slope = coefEst[2], col="blue") +
  xlab("Number of cigarattes smoked") +
  ylab("Risk index of CVD")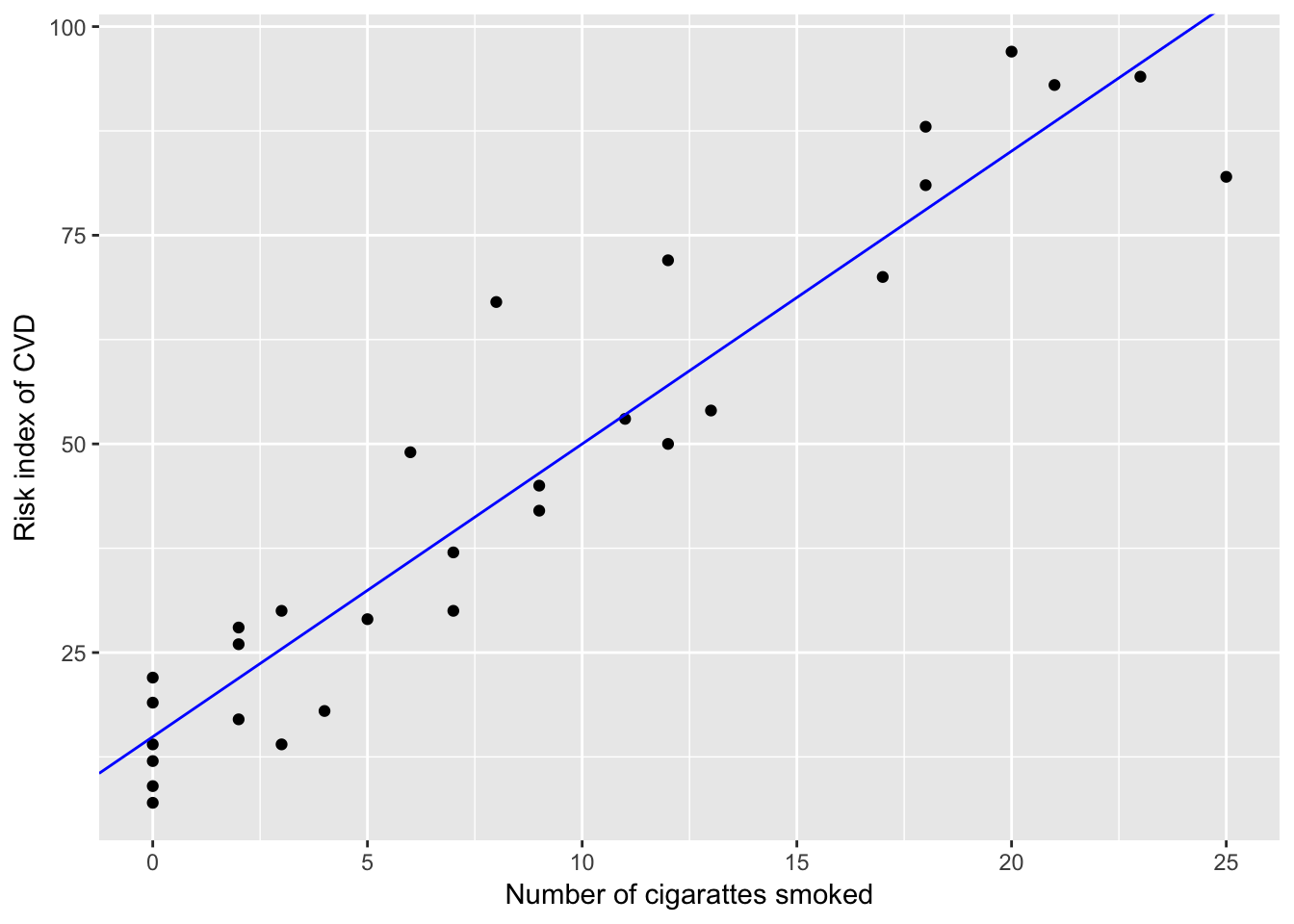

Problem 16.6 (b)

lmCov = lm(RISK~NOCIG+TREATMENT+NOCIG:TREATMENT, data=data165)
anova(lmCov)

## Analysis of Variance Table
## 
## Response: RISK
##                 Df  Sum Sq Mean Sq   F value    Pr(>F)    
## NOCIG            1 21410.9 21410.9 1055.3276 < 2.2e-16 ***
## TREATMENT        2  1820.1   910.1   44.8561 7.814e-09 ***
## NOCIG:TREATMENT  2   127.1    63.5    3.1319   0.06186 .  
## Residuals       24   486.9    20.3                        
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

pval = as.character(anova(lmCov)$`Pr(>F)`); pval

## [1] "2.37964027689756e-21" "7.81358987634045e-09" "0.0618641631946161"  
## [4] NA

The p-value for the interaction term (NOCIG:TREATMENT) is 0.0618641631946161 > 0.05. We cannot reject the \(H_{0}\) that the slopes for the three treatments are eqaul.

Below is a scatterplot grouped by treatments, also showing a very weak evidence of equal slopes for the three treatments.

coefC = coef(lm(RISK~NOCIG, data=data165[data165$TREATMENT=="C", ])); coefC

## (Intercept)       NOCIG 
##   22.040757    3.909753

coefI = coef(lm(RISK~NOCIG, data=data165[data165$TREATMENT=="I", ])); coefI

## (Intercept)       NOCIG 
##    8.334266    3.251748

coefII = coef(lm(RISK~NOCIG, data=data165[data165$TREATMENT=="II", ])); coefII

## (Intercept)       NOCIG 
##   11.610362    3.738504

ggplot(data165, aes(x=NOCIG, y=RISK, col=TREATMENT)) + 
  geom_point() +
  geom_abline(intercept = coefC[1], slope = coefC[2], col="red") +
  geom_abline(intercept = coefI[1], slope = coefI[2], col="green") +
  geom_abline(intercept = coefII[1], slope = coefII[2], col="blue") +
  xlab("Number of cigarattes smoked") +
  ylab("Risk index of CVD")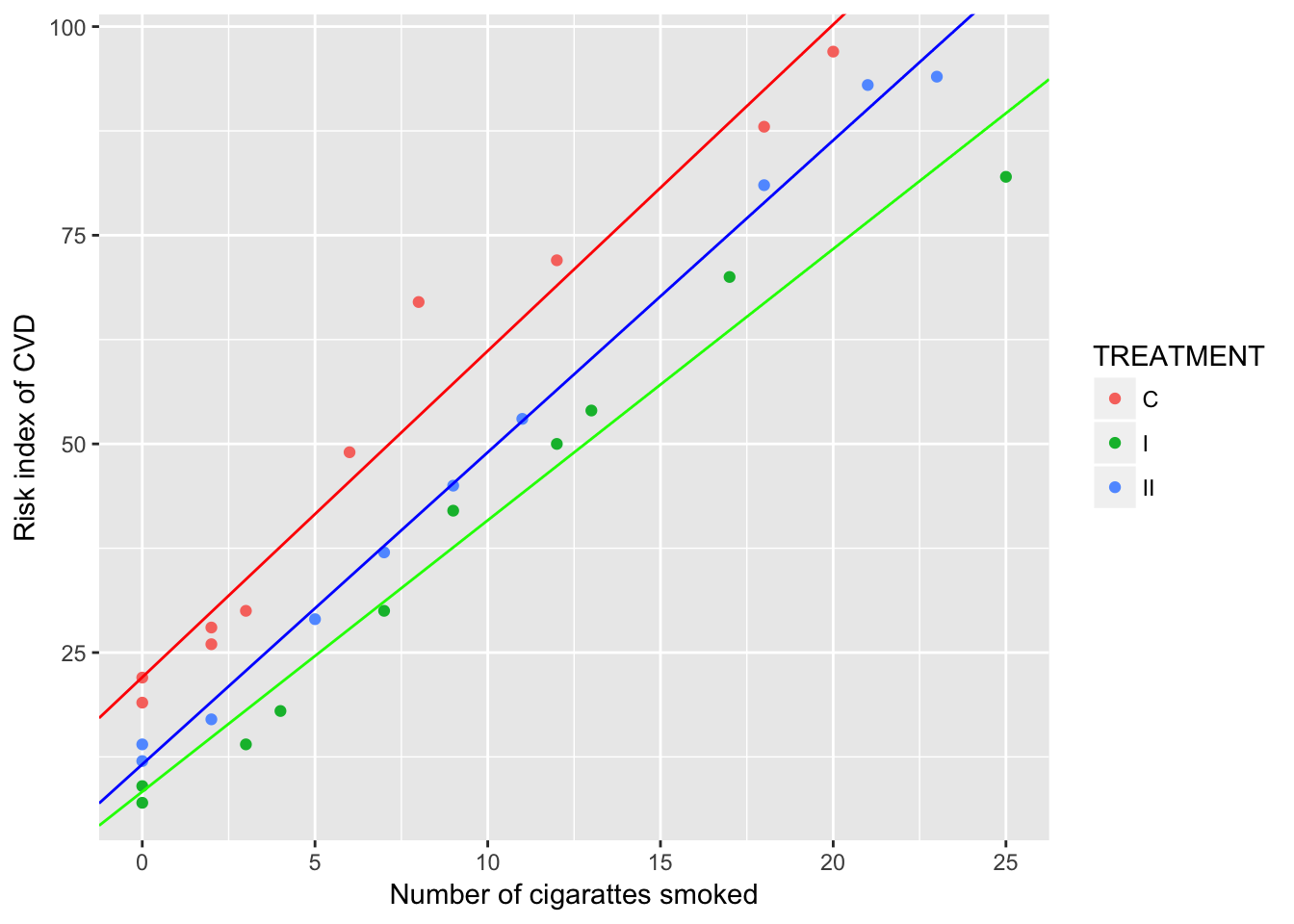

Problem 16.6 (b)

lmCov = lm(RISK~NOCIG+TREATMENT, data=data165)
anova(lmCov)

## Analysis of Variance Table
## 
## Response: RISK
##           Df  Sum Sq Mean Sq F value    Pr(>F)    
## NOCIG      1 21410.9 21410.9 906.642 < 2.2e-16 ***
## TREATMENT  2  1820.1   910.1  38.536 1.674e-08 ***
## Residuals 26   614.0    23.6                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

pval = as.character(anova(lmCov)$`Pr(>F)`); pval

## [1] "9.64564444508505e-22" "1.67413337584042e-08" NA

Yes. The p-value for TREATMENT is 1.67413337584042e-08, indicating a strong evidence of difference in the mean risk index for the three treatments.