9. Regression¶
Chinese proverb
A journey of a thousand miles begins with a single step. – old Chinese proverb
In statistical modeling, regression analysis focuses on investigating the relationship between a dependent variable and one or more independent variables. Wikipedia Regression analysis
In data mining, Regression is a model to represent the relationship between the value of lable ( or target, it is numerical variable) and on one or more features (or predictors they can be numerical and categorical variables).
9.1. Linear Regression¶
9.1.1. Introduction¶
Given that a data set 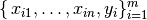 which contains n features (variables) and m samples (data points), in simple linear regression model for modeling
which contains n features (variables) and m samples (data points), in simple linear regression model for modeling 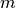 data points with
data points with 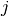 independent variables:
independent variables: 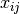 , the formula is given by:
, the formula is given by:
In matrix notation, the data set is written as ![\X = [\x_1,\cdots, \x_n]](_images/math/f3dccbc22308d3d31fa6cb52c6a71a00c90bb63a.png) with
with
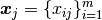 ,
,
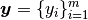 (see Fig. Feature matrix and label)
and
(see Fig. Feature matrix and label)
and 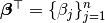 .
Then the matrix format equation is written as
.
Then the matrix format equation is written as
(1)¶
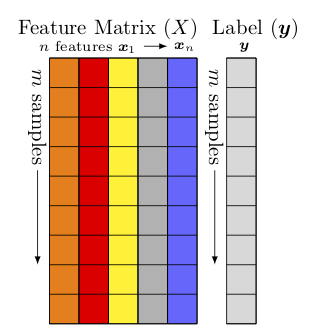
Feature matrix and label¶
9.1.2. How to solve it?¶
Direct Methods (For more information please refer to my Prelim Notes for Numerical Analysis)
For squared or rectangular matrices
Singular Value Decomposition
Gram-Schmidt orthogonalization
QR Decomposition
For squared matrices
LU Decomposition
Cholesky Decomposition
Regular Splittings
Iterative Methods
Stationary cases iterative method
Jacobi Method
Gauss-Seidel Method
Richardson Method
Successive Over Relaxation (SOR) Method
Dynamic cases iterative method
Chebyshev iterative Method
Minimal residuals Method
Minimal correction iterative method
Steepest Descent Method
Conjugate Gradients Method
9.1.3. Ordinary Least Squares¶
In mathematics, (1) is a overdetermined system. The method of ordinary least squares can be used to find an approximate solution to overdetermined systems. For the system overdetermined system (1), the least squares formula is obtained from the problem
(2)¶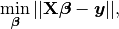
the solution of which can be written with the normal equations:
(3)¶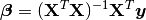
where 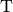 indicates a matrix transpose, provided
indicates a matrix transpose, provided 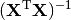 exists (that is, provided
exists (that is, provided 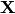 has full column rank).
has full column rank).
9.1.4. Gradient Descent¶
Let’s use the following hypothesis:
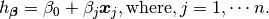
Then, solving (2) is equivalent to minimize the following cost fucntion :
9.1.5. Cost Function¶
(4)¶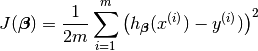
Note
The reason why we prefer to solve (4) rather than (2) is because (4) is convex and it has some nice properties, such as it’s uniquely solvable and energy stable for small enough learning rate. the interested reader who has great interest in non-convex cost function (energy) case. is referred to [Feng2016PSD] for more details.
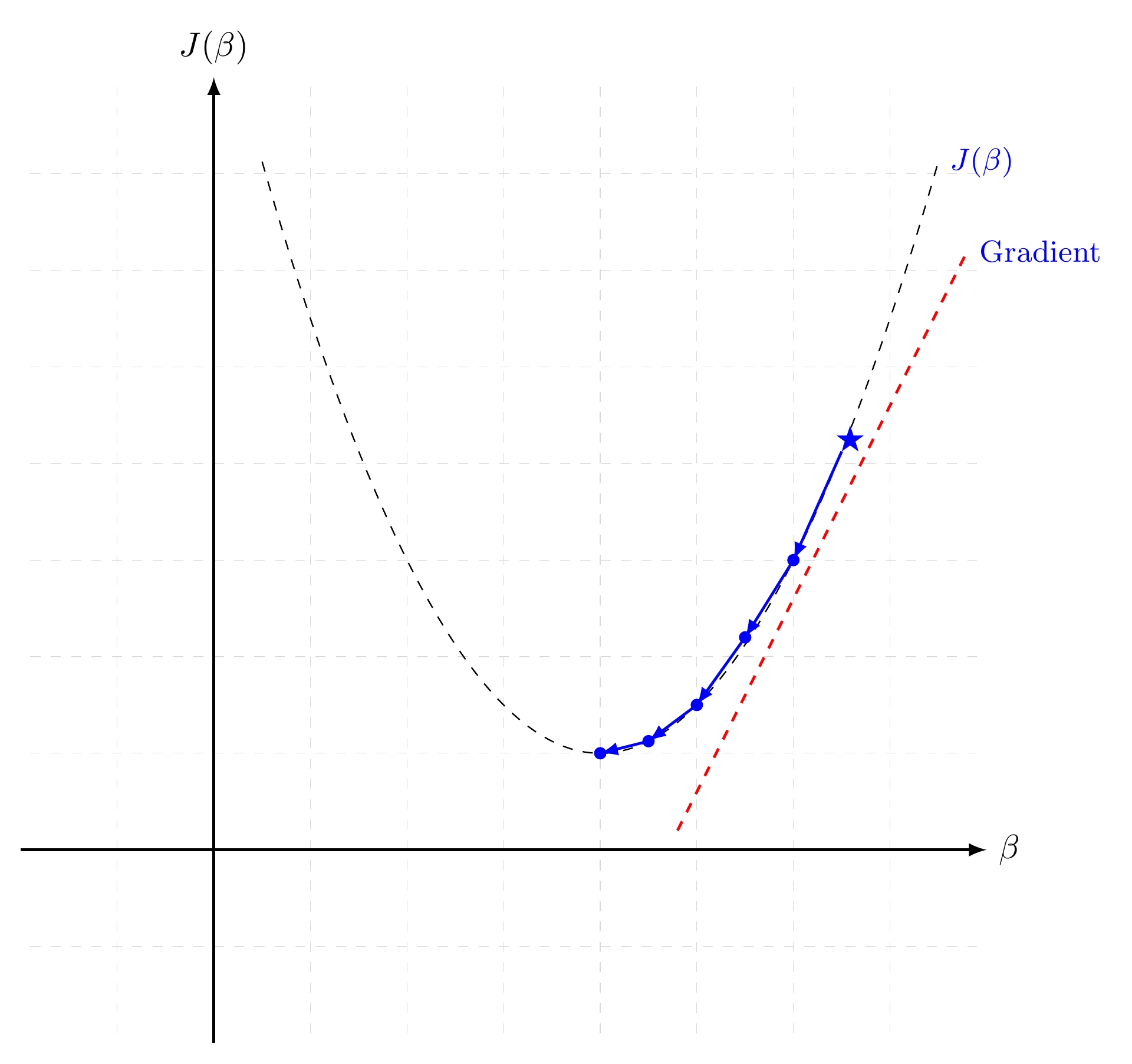
Gradient Descent in 1D¶
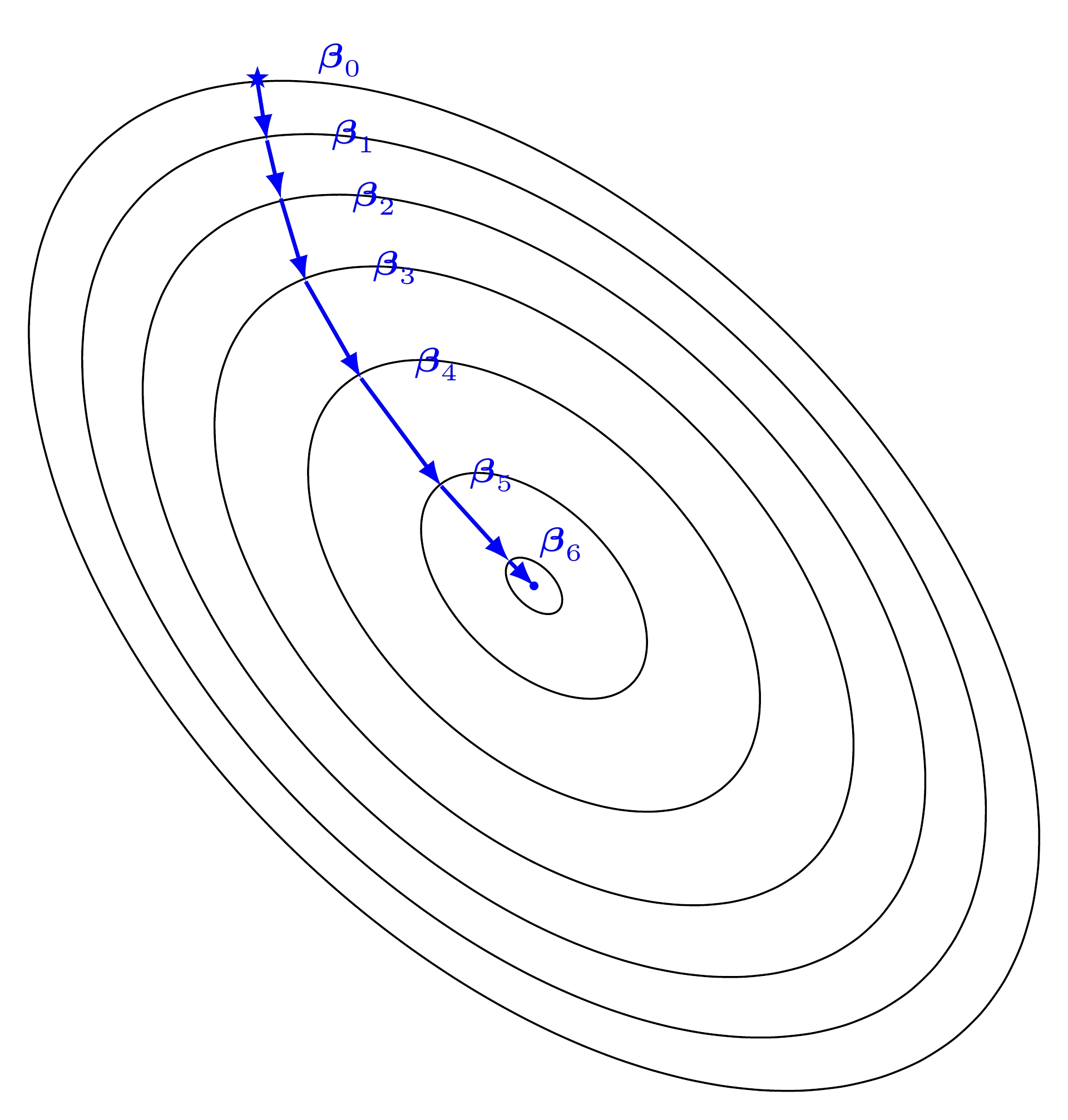
Gradient Descent in 2D¶
9.1.6. Batch Gradient Descent¶
Gradient descent is a first-order iterative optimization algorithm for finding the minimum of a function. It searchs with the direction of the steepest desscent which is defined by the negative of the gradient (see Fig. Gradient Descent in 1D and Gradient Descent in 2D for 1D and 2D, respectively) and with learning rate (search step) 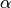 .
.
9.1.7. Stochastic Dradient Descent¶
9.1.8. Mini-batch Gradient Descent¶
9.1.9. Demo¶
The Jupyter notebook can be download from Linear Regression which was implemented without using Pipeline.
The Jupyter notebook can be download from Linear Regression with Pipeline which was implemented with using Pipeline.
I will only present the code with pipeline style in the following.
For more details about the parameters, please visit Linear Regression API .
Set up spark context and SparkSession
from pyspark.sql import SparkSession
spark = SparkSession \
.builder \
.appName("Python Spark regression example") \
.config("spark.some.config.option", "some-value") \
.getOrCreate()
Load dataset
df = spark.read.format('com.databricks.spark.csv').\
options(header='true', \
inferschema='true').\
load("../data/Advertising.csv",header=True);
check the data set
df.show(5,True)
df.printSchema()
Then you will get
+-----+-----+---------+-----+
| TV|Radio|Newspaper|Sales|
+-----+-----+---------+-----+
|230.1| 37.8| 69.2| 22.1|
| 44.5| 39.3| 45.1| 10.4|
| 17.2| 45.9| 69.3| 9.3|
|151.5| 41.3| 58.5| 18.5|
|180.8| 10.8| 58.4| 12.9|
+-----+-----+---------+-----+
only showing top 5 rows
root
|-- TV: double (nullable = true)
|-- Radio: double (nullable = true)
|-- Newspaper: double (nullable = true)
|-- Sales: double (nullable = true)
You can also get the Statistical results from the data frame (Unfortunately, it only works for numerical).
df.describe().show()
Then you will get
+-------+-----------------+------------------+------------------+------------------+
|summary| TV| Radio| Newspaper| Sales|
+-------+-----------------+------------------+------------------+------------------+
| count| 200| 200| 200| 200|
| mean| 147.0425|23.264000000000024|30.553999999999995|14.022500000000003|
| stddev|85.85423631490805|14.846809176168728| 21.77862083852283| 5.217456565710477|
| min| 0.7| 0.0| 0.3| 1.6|
| max| 296.4| 49.6| 114.0| 27.0|
+-------+-----------------+------------------+------------------+------------------+
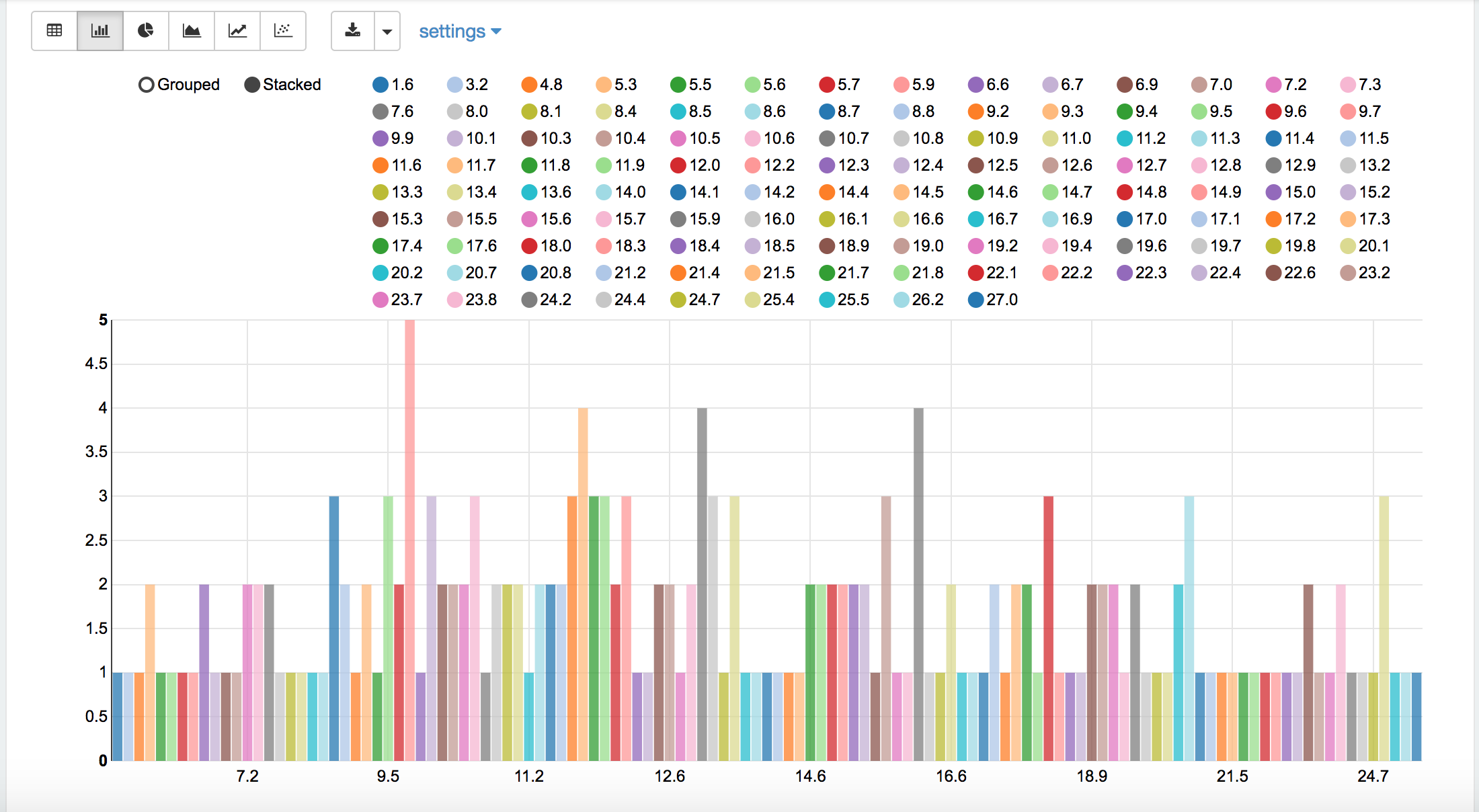
Sales distribution¶
Convert the data to dense vector (features and label)
from pyspark.sql import Row
from pyspark.ml.linalg import Vectors
# I provide two ways to build the features and labels
# method 1 (good for small feature):
#def transData(row):
# return Row(label=row["Sales"],
# features=Vectors.dense([row["TV"],
# row["Radio"],
# row["Newspaper"]]))
# Method 2 (good for large features):
def transData(data):
return data.rdd.map(lambda r: [Vectors.dense(r[:-1]),r[-1]]).toDF(['features','label'])
Note
You are strongly encouraged to try my
get_dummyfunction for dealing with the categorical data in comple dataset.Supervised learning version:
def get_dummy(df,indexCol,categoricalCols,continuousCols,labelCol): from pyspark.ml import Pipeline from pyspark.ml.feature import StringIndexer, OneHotEncoder, VectorAssembler from pyspark.sql.functions import col indexers = [ StringIndexer(inputCol=c, outputCol="{0}_indexed".format(c)) for c in categoricalCols ] # default setting: dropLast=True encoders = [ OneHotEncoder(inputCol=indexer.getOutputCol(), outputCol="{0}_encoded".format(indexer.getOutputCol())) for indexer in indexers ] assembler = VectorAssembler(inputCols=[encoder.getOutputCol() for encoder in encoders] + continuousCols, outputCol="features") pipeline = Pipeline(stages=indexers + encoders + [assembler]) model=pipeline.fit(df) data = model.transform(df) data = data.withColumn('label',col(labelCol)) if indexCol: return data.select(indexCol,'features','label') else: return data.select('features','label')Unsupervised learning version:
def get_dummy(df,indexCol,categoricalCols,continuousCols): ''' Get dummy variables and concat with continuous variables for unsupervised learning. :param df: the dataframe :param categoricalCols: the name list of the categorical data :param continuousCols: the name list of the numerical data :return k: feature matrix :author: Wenqiang Feng :email: von198@gmail.com ''' indexers = [ StringIndexer(inputCol=c, outputCol="{0}_indexed".format(c)) for c in categoricalCols ] # default setting: dropLast=True encoders = [ OneHotEncoder(inputCol=indexer.getOutputCol(), outputCol="{0}_encoded".format(indexer.getOutputCol())) for indexer in indexers ] assembler = VectorAssembler(inputCols=[encoder.getOutputCol() for encoder in encoders] + continuousCols, outputCol="features") pipeline = Pipeline(stages=indexers + encoders + [assembler]) model=pipeline.fit(df) data = model.transform(df) if indexCol: return data.select(indexCol,'features') else: return data.select('features')
Two in one:
def get_dummy(df,indexCol,categoricalCols,continuousCols,labelCol,dropLast=False): ''' Get dummy variables and concat with continuous variables for ml modeling. :param df: the dataframe :param categoricalCols: the name list of the categorical data :param continuousCols: the name list of the numerical data :param labelCol: the name of label column :param dropLast: the flag of drop last column :return: feature matrix :author: Wenqiang Feng :email: von198@gmail.com >>> df = spark.createDataFrame([ (0, "a"), (1, "b"), (2, "c"), (3, "a"), (4, "a"), (5, "c") ], ["id", "category"]) >>> indexCol = 'id' >>> categoricalCols = ['category'] >>> continuousCols = [] >>> labelCol = [] >>> mat = get_dummy(df,indexCol,categoricalCols,continuousCols,labelCol) >>> mat.show() >>> +---+-------------+ | id| features| +---+-------------+ | 0|[1.0,0.0,0.0]| | 1|[0.0,0.0,1.0]| | 2|[0.0,1.0,0.0]| | 3|[1.0,0.0,0.0]| | 4|[1.0,0.0,0.0]| | 5|[0.0,1.0,0.0]| +---+-------------+ ''' from pyspark.ml import Pipeline from pyspark.ml.feature import StringIndexer, OneHotEncoder, VectorAssembler from pyspark.sql.functions import col indexers = [ StringIndexer(inputCol=c, outputCol="{0}_indexed".format(c)) for c in categoricalCols ] # default setting: dropLast=True encoders = [ OneHotEncoder(inputCol=indexer.getOutputCol(), outputCol="{0}_encoded".format(indexer.getOutputCol()),dropLast=dropLast) for indexer in indexers ] assembler = VectorAssembler(inputCols=[encoder.getOutputCol() for encoder in encoders] + continuousCols, outputCol="features") pipeline = Pipeline(stages=indexers + encoders + [assembler]) model=pipeline.fit(df) data = model.transform(df) if indexCol and labelCol: # for supervised learning data = data.withColumn('label',col(labelCol)) return data.select(indexCol,'features','label') elif not indexCol and labelCol: # for supervised learning data = data.withColumn('label',col(labelCol)) return data.select('features','label') elif indexCol and not labelCol: # for unsupervised learning return data.select(indexCol,'features') elif not indexCol and not labelCol: # for unsupervised learning return data.select('features')
Transform the dataset to DataFrame
transformed= transData(df)
transformed.show(5)
+-----------------+-----+
| features|label|
+-----------------+-----+
|[230.1,37.8,69.2]| 22.1|
| [44.5,39.3,45.1]| 10.4|
| [17.2,45.9,69.3]| 9.3|
|[151.5,41.3,58.5]| 18.5|
|[180.8,10.8,58.4]| 12.9|
+-----------------+-----+
only showing top 5 rows
Note
You will find out that all of the supervised machine learning algorithms in Spark are based on the features and label (unsupervised machine learning algorithms in Spark are based on the features). That is to say, you can play with all of the machine learning algorithms in Spark when you get ready the features and label in pipeline architecture.
Deal With Categorical Variables
from pyspark.ml import Pipeline
from pyspark.ml.regression import LinearRegression
from pyspark.ml.feature import VectorIndexer
from pyspark.ml.evaluation import RegressionEvaluator
# Automatically identify categorical features, and index them.
# We specify maxCategories so features with > 4 distinct values are treated as continuous.
featureIndexer = VectorIndexer(inputCol="features", \
outputCol="indexedFeatures",\
maxCategories=4).fit(transformed)
data = featureIndexer.transform(transformed)
Now you check your dataset with
data.show(5,True)
you will get
+-----------------+-----+-----------------+
| features|label| indexedFeatures|
+-----------------+-----+-----------------+
|[230.1,37.8,69.2]| 22.1|[230.1,37.8,69.2]|
| [44.5,39.3,45.1]| 10.4| [44.5,39.3,45.1]|
| [17.2,45.9,69.3]| 9.3| [17.2,45.9,69.3]|
|[151.5,41.3,58.5]| 18.5|[151.5,41.3,58.5]|
|[180.8,10.8,58.4]| 12.9|[180.8,10.8,58.4]|
+-----------------+-----+-----------------+
only showing top 5 rows
Split the data into training and test sets (40% held out for testing)
# Split the data into training and test sets (40% held out for testing)
(trainingData, testData) = transformed.randomSplit([0.6, 0.4])
You can check your train and test data as follows (In my opinion, it is always to good to keep tracking your data during prototype pahse):
trainingData.show(5)
testData.show(5)
Then you will get
+---------------+-----+---------------+
| features|label|indexedFeatures|
+---------------+-----+---------------+
| [4.1,11.6,5.7]| 3.2| [4.1,11.6,5.7]|
| [5.4,29.9,9.4]| 5.3| [5.4,29.9,9.4]|
|[7.3,28.1,41.4]| 5.5|[7.3,28.1,41.4]|
|[7.8,38.9,50.6]| 6.6|[7.8,38.9,50.6]|
| [8.6,2.1,1.0]| 4.8| [8.6,2.1,1.0]|
+---------------+-----+---------------+
only showing top 5 rows
+----------------+-----+----------------+
| features|label| indexedFeatures|
+----------------+-----+----------------+
| [0.7,39.6,8.7]| 1.6| [0.7,39.6,8.7]|
| [8.4,27.2,2.1]| 5.7| [8.4,27.2,2.1]|
|[11.7,36.9,45.2]| 7.3|[11.7,36.9,45.2]|
|[13.2,15.9,49.6]| 5.6|[13.2,15.9,49.6]|
|[16.9,43.7,89.4]| 8.7|[16.9,43.7,89.4]|
+----------------+-----+----------------+
only showing top 5 rows
Fit Ordinary Least Square Regression Model
For more details about the parameters, please visit Linear Regression API .
# Import LinearRegression class
from pyspark.ml.regression import LinearRegression
# Define LinearRegression algorithm
lr = LinearRegression()
Pipeline Architecture
# Chain indexer and tree in a Pipeline
pipeline = Pipeline(stages=[featureIndexer, lr])
model = pipeline.fit(trainingData)
Summary of the Model
Spark has a poor summary function for data and model. I wrote a summary function which has similar format as R output for the linear regression in PySpark.
def modelsummary(model):
import numpy as np
print ("Note: the last rows are the information for Intercept")
print ("##","-------------------------------------------------")
print ("##"," Estimate | Std.Error | t Values | P-value")
coef = np.append(list(model.coefficients),model.intercept)
Summary=model.summary
for i in range(len(Summary.pValues)):
print ("##",'{:10.6f}'.format(coef[i]),\
'{:10.6f}'.format(Summary.coefficientStandardErrors[i]),\
'{:8.3f}'.format(Summary.tValues[i]),\
'{:10.6f}'.format(Summary.pValues[i]))
print ("##",'---')
print ("##","Mean squared error: % .6f" \
% Summary.meanSquaredError, ", RMSE: % .6f" \
% Summary.rootMeanSquaredError )
print ("##","Multiple R-squared: %f" % Summary.r2, ", \
Total iterations: %i"% Summary.totalIterations)
modelsummary(model.stages[-1])
You will get the following summary results:
Note: the last rows are the information for Intercept
('##', '-------------------------------------------------')
('##', ' Estimate | Std.Error | t Values | P-value')
('##', ' 0.044186', ' 0.001663', ' 26.573', ' 0.000000')
('##', ' 0.206311', ' 0.010846', ' 19.022', ' 0.000000')
('##', ' 0.001963', ' 0.007467', ' 0.263', ' 0.793113')
('##', ' 2.596154', ' 0.379550', ' 6.840', ' 0.000000')
('##', '---')
('##', 'Mean squared error: 2.588230', ', RMSE: 1.608798')
('##', 'Multiple R-squared: 0.911869', ', Total iterations: 1')
Make predictions
# Make predictions.
predictions = model.transform(testData)
# Select example rows to display.
predictions.select("features","label","prediction").show(5)
+----------------+-----+------------------+
| features|label| prediction|
+----------------+-----+------------------+
| [0.7,39.6,8.7]| 1.6| 10.81405928637388|
| [8.4,27.2,2.1]| 5.7| 8.583086404079918|
|[11.7,36.9,45.2]| 7.3|10.814712818232422|
|[13.2,15.9,49.6]| 5.6| 6.557106943899219|
|[16.9,43.7,89.4]| 8.7|12.534151375058645|
+----------------+-----+------------------+
only showing top 5 rows
Evaluation
from pyspark.ml.evaluation import RegressionEvaluator
# Select (prediction, true label) and compute test error
evaluator = RegressionEvaluator(labelCol="label",
predictionCol="prediction",
metricName="rmse")
rmse = evaluator.evaluate(predictions)
print("Root Mean Squared Error (RMSE) on test data = %g" % rmse)
The final Root Mean Squared Error (RMSE) is as follows:
Root Mean Squared Error (RMSE) on test data = 1.63114
You can also check the 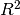 value for the test data:
value for the test data:
y_true = predictions.select("label").toPandas()
y_pred = predictions.select("prediction").toPandas()
import sklearn.metrics
r2_score = sklearn.metrics.r2_score(y_true, y_pred)
print('r2_score: {0}'.format(r2_score))
Then you will get
r2_score: 0.854486655585
Warning
You should know most softwares are using different formula to calculate the
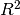 value when no intercept is included in the model. You can get more
information from the disscussion at StackExchange.
value when no intercept is included in the model. You can get more
information from the disscussion at StackExchange.
9.2. Generalized linear regression¶
9.2.1. Introduction¶
9.2.2. How to solve it?¶
9.2.3. Demo¶
The Jupyter notebook can be download from Generalized Linear Regression.
For more details about the parameters, please visit Generalized Linear Regression API .
Set up spark context and SparkSession
from pyspark.sql import SparkSession
spark = SparkSession \
.builder \
.appName("Python Spark regression example") \
.config("spark.some.config.option", "some-value") \
.getOrCreate()
Load dataset
df = spark.read.format('com.databricks.spark.csv').\
options(header='true', \
inferschema='true').\
load("../data/Advertising.csv",header=True);
check the data set
df.show(5,True)
df.printSchema()
Then you will get
+-----+-----+---------+-----+
| TV|Radio|Newspaper|Sales|
+-----+-----+---------+-----+
|230.1| 37.8| 69.2| 22.1|
| 44.5| 39.3| 45.1| 10.4|
| 17.2| 45.9| 69.3| 9.3|
|151.5| 41.3| 58.5| 18.5|
|180.8| 10.8| 58.4| 12.9|
+-----+-----+---------+-----+
only showing top 5 rows
root
|-- TV: double (nullable = true)
|-- Radio: double (nullable = true)
|-- Newspaper: double (nullable = true)
|-- Sales: double (nullable = true)
You can also get the Statistical resutls from the data frame (Unfortunately, it only works for numerical).
df.describe().show()
Then you will get
+-------+-----------------+------------------+------------------+------------------+
|summary| TV| Radio| Newspaper| Sales|
+-------+-----------------+------------------+------------------+------------------+
| count| 200| 200| 200| 200|
| mean| 147.0425|23.264000000000024|30.553999999999995|14.022500000000003|
| stddev|85.85423631490805|14.846809176168728| 21.77862083852283| 5.217456565710477|
| min| 0.7| 0.0| 0.3| 1.6|
| max| 296.4| 49.6| 114.0| 27.0|
+-------+-----------------+------------------+------------------+------------------+
Convert the data to dense vector (features and label)
Note
You are strongly encouraged to try my
get_dummyfunction for dealing with the categorical data in comple dataset.Supervised learning version:
def get_dummy(df,indexCol,categoricalCols,continuousCols,labelCol): from pyspark.ml import Pipeline from pyspark.ml.feature import StringIndexer, OneHotEncoder, VectorAssembler from pyspark.sql.functions import col indexers = [ StringIndexer(inputCol=c, outputCol="{0}_indexed".format(c)) for c in categoricalCols ] # default setting: dropLast=True encoders = [ OneHotEncoder(inputCol=indexer.getOutputCol(), outputCol="{0}_encoded".format(indexer.getOutputCol())) for indexer in indexers ] assembler = VectorAssembler(inputCols=[encoder.getOutputCol() for encoder in encoders] + continuousCols, outputCol="features") pipeline = Pipeline(stages=indexers + encoders + [assembler]) model=pipeline.fit(df) data = model.transform(df) data = data.withColumn('label',col(labelCol)) if indexCol: return data.select(indexCol,'features','label') else: return data.select('features','label')Unsupervised learning version:
def get_dummy(df,indexCol,categoricalCols,continuousCols): ''' Get dummy variables and concat with continuous variables for unsupervised learning. :param df: the dataframe :param categoricalCols: the name list of the categorical data :param continuousCols: the name list of the numerical data :return k: feature matrix :author: Wenqiang Feng :email: von198@gmail.com ''' indexers = [ StringIndexer(inputCol=c, outputCol="{0}_indexed".format(c)) for c in categoricalCols ] # default setting: dropLast=True encoders = [ OneHotEncoder(inputCol=indexer.getOutputCol(), outputCol="{0}_encoded".format(indexer.getOutputCol())) for indexer in indexers ] assembler = VectorAssembler(inputCols=[encoder.getOutputCol() for encoder in encoders] + continuousCols, outputCol="features") pipeline = Pipeline(stages=indexers + encoders + [assembler]) model=pipeline.fit(df) data = model.transform(df) if indexCol: return data.select(indexCol,'features') else: return data.select('features')
Two in one:
def get_dummy(df,indexCol,categoricalCols,continuousCols,labelCol,dropLast=False): ''' Get dummy variables and concat with continuous variables for ml modeling. :param df: the dataframe :param categoricalCols: the name list of the categorical data :param continuousCols: the name list of the numerical data :param labelCol: the name of label column :param dropLast: the flag of drop last column :return: feature matrix :author: Wenqiang Feng :email: von198@gmail.com >>> df = spark.createDataFrame([ (0, "a"), (1, "b"), (2, "c"), (3, "a"), (4, "a"), (5, "c") ], ["id", "category"]) >>> indexCol = 'id' >>> categoricalCols = ['category'] >>> continuousCols = [] >>> labelCol = [] >>> mat = get_dummy(df,indexCol,categoricalCols,continuousCols,labelCol) >>> mat.show() >>> +---+-------------+ | id| features| +---+-------------+ | 0|[1.0,0.0,0.0]| | 1|[0.0,0.0,1.0]| | 2|[0.0,1.0,0.0]| | 3|[1.0,0.0,0.0]| | 4|[1.0,0.0,0.0]| | 5|[0.0,1.0,0.0]| +---+-------------+ ''' from pyspark.ml import Pipeline from pyspark.ml.feature import StringIndexer, OneHotEncoder, VectorAssembler from pyspark.sql.functions import col indexers = [ StringIndexer(inputCol=c, outputCol="{0}_indexed".format(c)) for c in categoricalCols ] # default setting: dropLast=True encoders = [ OneHotEncoder(inputCol=indexer.getOutputCol(), outputCol="{0}_encoded".format(indexer.getOutputCol()),dropLast=dropLast) for indexer in indexers ] assembler = VectorAssembler(inputCols=[encoder.getOutputCol() for encoder in encoders] + continuousCols, outputCol="features") pipeline = Pipeline(stages=indexers + encoders + [assembler]) model=pipeline.fit(df) data = model.transform(df) if indexCol and labelCol: # for supervised learning data = data.withColumn('label',col(labelCol)) return data.select(indexCol,'features','label') elif not indexCol and labelCol: # for supervised learning data = data.withColumn('label',col(labelCol)) return data.select('features','label') elif indexCol and not labelCol: # for unsupervised learning return data.select(indexCol,'features') elif not indexCol and not labelCol: # for unsupervised learning return data.select('features')
from pyspark.sql import Row
from pyspark.ml.linalg import Vectors
# I provide two ways to build the features and labels
# method 1 (good for small feature):
#def transData(row):
# return Row(label=row["Sales"],
# features=Vectors.dense([row["TV"],
# row["Radio"],
# row["Newspaper"]]))
# Method 2 (good for large features):
def transData(data):
return data.rdd.map(lambda r: [Vectors.dense(r[:-1]),r[-1]]).toDF(['features','label'])
transformed= transData(df)
transformed.show(5)
+-----------------+-----+
| features|label|
+-----------------+-----+
|[230.1,37.8,69.2]| 22.1|
| [44.5,39.3,45.1]| 10.4|
| [17.2,45.9,69.3]| 9.3|
|[151.5,41.3,58.5]| 18.5|
|[180.8,10.8,58.4]| 12.9|
+-----------------+-----+
only showing top 5 rows
Note
You will find out that all of the machine learning algorithms in Spark are based on the features and label. That is to say, you can play with all of the machine learning algorithms in Spark when you get ready the features and label.
Convert the data to dense vector
# convert the data to dense vector
def transData(data):
return data.rdd.map(lambda r: [r[-1], Vectors.dense(r[:-1])]).\
toDF(['label','features'])
from pyspark.sql import Row
from pyspark.ml.linalg import Vectors
data= transData(df)
data.show()
Deal with the Categorical variables
from pyspark.ml import Pipeline
from pyspark.ml.regression import LinearRegression
from pyspark.ml.feature import VectorIndexer
from pyspark.ml.evaluation import RegressionEvaluator
# Automatically identify categorical features, and index them.
# We specify maxCategories so features with > 4
# distinct values are treated as continuous.
featureIndexer = VectorIndexer(inputCol="features", \
outputCol="indexedFeatures",\
maxCategories=4).fit(transformed)
data = featureIndexer.transform(transformed)
When you check you data at this point, you will get
+-----------------+-----+-----------------+
| features|label| indexedFeatures|
+-----------------+-----+-----------------+
|[230.1,37.8,69.2]| 22.1|[230.1,37.8,69.2]|
| [44.5,39.3,45.1]| 10.4| [44.5,39.3,45.1]|
| [17.2,45.9,69.3]| 9.3| [17.2,45.9,69.3]|
|[151.5,41.3,58.5]| 18.5|[151.5,41.3,58.5]|
|[180.8,10.8,58.4]| 12.9|[180.8,10.8,58.4]|
+-----------------+-----+-----------------+
only showing top 5 rows
Split the data into training and test sets (40% held out for testing)
# Split the data into training and test sets (40% held out for testing)
(trainingData, testData) = transformed.randomSplit([0.6, 0.4])
You can check your train and test data as follows (In my opinion, it is always to good to keep tracking your data during prototype phase):
trainingData.show(5)
testData.show(5)
Then you will get
+----------------+-----+----------------+
| features|label| indexedFeatures|
+----------------+-----+----------------+
| [5.4,29.9,9.4]| 5.3| [5.4,29.9,9.4]|
| [7.8,38.9,50.6]| 6.6| [7.8,38.9,50.6]|
| [8.4,27.2,2.1]| 5.7| [8.4,27.2,2.1]|
| [8.7,48.9,75.0]| 7.2| [8.7,48.9,75.0]|
|[11.7,36.9,45.2]| 7.3|[11.7,36.9,45.2]|
+----------------+-----+----------------+
only showing top 5 rows
+---------------+-----+---------------+
| features|label|indexedFeatures|
+---------------+-----+---------------+
| [0.7,39.6,8.7]| 1.6| [0.7,39.6,8.7]|
| [4.1,11.6,5.7]| 3.2| [4.1,11.6,5.7]|
|[7.3,28.1,41.4]| 5.5|[7.3,28.1,41.4]|
| [8.6,2.1,1.0]| 4.8| [8.6,2.1,1.0]|
|[17.2,4.1,31.6]| 5.9|[17.2,4.1,31.6]|
+---------------+-----+---------------+
only showing top 5 rows
Fit Generalized Linear Regression Model
# Import LinearRegression class
from pyspark.ml.regression import GeneralizedLinearRegression
# Define LinearRegression algorithm
glr = GeneralizedLinearRegression(family="gaussian", link="identity",\
maxIter=10, regParam=0.3)
Pipeline Architecture
# Chain indexer and tree in a Pipeline
pipeline = Pipeline(stages=[featureIndexer, glr])
model = pipeline.fit(trainingData)
Summary of the Model
Spark has a poor summary function for data and model. I wrote a summary function which has similar format as R output for the linear regression in PySpark.
def modelsummary(model):
import numpy as np
print ("Note: the last rows are the information for Intercept")
print ("##","-------------------------------------------------")
print ("##"," Estimate | Std.Error | t Values | P-value")
coef = np.append(list(model.coefficients),model.intercept)
Summary=model.summary
for i in range(len(Summary.pValues)):
print ("##",'{:10.6f}'.format(coef[i]),\
'{:10.6f}'.format(Summary.coefficientStandardErrors[i]),\
'{:8.3f}'.format(Summary.tValues[i]),\
'{:10.6f}'.format(Summary.pValues[i]))
print ("##",'---')
# print ("##","Mean squared error: % .6f" \
# % Summary.meanSquaredError, ", RMSE: % .6f" \
# % Summary.rootMeanSquaredError )
# print ("##","Multiple R-squared: %f" % Summary.r2, ", \
# Total iterations: %i"% Summary.totalIterations)
modelsummary(model.stages[-1])
You will get the following summary results:
Note: the last rows are the information for Intercept
('##', '-------------------------------------------------')
('##', ' Estimate | Std.Error | t Values | P-value')
('##', ' 0.042857', ' 0.001668', ' 25.692', ' 0.000000')
('##', ' 0.199922', ' 0.009881', ' 20.232', ' 0.000000')
('##', ' -0.001957', ' 0.006917', ' -0.283', ' 0.777757')
('##', ' 3.007515', ' 0.406389', ' 7.401', ' 0.000000')
('##', '---')
Make predictions
# Make predictions.
predictions = model.transform(testData)
# Select example rows to display.
predictions.select("features","label","predictedLabel").show(5)
+---------------+-----+------------------+
| features|label| prediction|
+---------------+-----+------------------+
| [0.7,39.6,8.7]| 1.6|10.937383732327625|
| [4.1,11.6,5.7]| 3.2| 5.491166258750164|
|[7.3,28.1,41.4]| 5.5| 8.8571603947873|
| [8.6,2.1,1.0]| 4.8| 3.793966281660073|
|[17.2,4.1,31.6]| 5.9| 4.502507124763654|
+---------------+-----+------------------+
only showing top 5 rows
Evaluation
from pyspark.ml.evaluation import RegressionEvaluator
from pyspark.ml.evaluation import RegressionEvaluator
# Select (prediction, true label) and compute test error
evaluator = RegressionEvaluator(labelCol="label",
predictionCol="prediction",
metricName="rmse")
rmse = evaluator.evaluate(predictions)
print("Root Mean Squared Error (RMSE) on test data = %g" % rmse)
The final Root Mean Squared Error (RMSE) is as follows:
Root Mean Squared Error (RMSE) on test data = 1.89857
y_true = predictions.select("label").toPandas()
y_pred = predictions.select("prediction").toPandas()
import sklearn.metrics
r2_score = sklearn.metrics.r2_score(y_true, y_pred)
print('r2_score: {0}'.format(r2_score))
Then you will get the 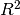 value:
value:
r2_score: 0.87707391843
9.3. Decision tree Regression¶
9.3.1. Introduction¶
9.3.2. How to solve it?¶
9.3.3. Demo¶
The Jupyter notebook can be download from Decision Tree Regression.
For more details about the parameters, please visit Decision Tree Regressor API .
Set up spark context and SparkSession
from pyspark.sql import SparkSession
spark = SparkSession \
.builder \
.appName("Python Spark regression example") \
.config("spark.some.config.option", "some-value") \
.getOrCreate()
Load dataset
df = spark.read.format('com.databricks.spark.csv').\
options(header='true', \
inferschema='true').\
load("../data/Advertising.csv",header=True);
check the data set
df.show(5,True)
df.printSchema()
Then you will get
+-----+-----+---------+-----+
| TV|Radio|Newspaper|Sales|
+-----+-----+---------+-----+
|230.1| 37.8| 69.2| 22.1|
| 44.5| 39.3| 45.1| 10.4|
| 17.2| 45.9| 69.3| 9.3|
|151.5| 41.3| 58.5| 18.5|
|180.8| 10.8| 58.4| 12.9|
+-----+-----+---------+-----+
only showing top 5 rows
root
|-- TV: double (nullable = true)
|-- Radio: double (nullable = true)
|-- Newspaper: double (nullable = true)
|-- Sales: double (nullable = true)
You can also get the Statistical resutls from the data frame (Unfortunately, it only works for numerical).
df.describe().show()
Then you will get
+-------+-----------------+------------------+------------------+------------------+
|summary| TV| Radio| Newspaper| Sales|
+-------+-----------------+------------------+------------------+------------------+
| count| 200| 200| 200| 200|
| mean| 147.0425|23.264000000000024|30.553999999999995|14.022500000000003|
| stddev|85.85423631490805|14.846809176168728| 21.77862083852283| 5.217456565710477|
| min| 0.7| 0.0| 0.3| 1.6|
| max| 296.4| 49.6| 114.0| 27.0|
+-------+-----------------+------------------+------------------+------------------+
Convert the data to dense vector (features and label)
Note
You are strongly encouraged to try my
get_dummyfunction for dealing with the categorical data in comple dataset.Supervised learning version:
def get_dummy(df,indexCol,categoricalCols,continuousCols,labelCol): from pyspark.ml import Pipeline from pyspark.ml.feature import StringIndexer, OneHotEncoder, VectorAssembler from pyspark.sql.functions import col indexers = [ StringIndexer(inputCol=c, outputCol="{0}_indexed".format(c)) for c in categoricalCols ] # default setting: dropLast=True encoders = [ OneHotEncoder(inputCol=indexer.getOutputCol(), outputCol="{0}_encoded".format(indexer.getOutputCol())) for indexer in indexers ] assembler = VectorAssembler(inputCols=[encoder.getOutputCol() for encoder in encoders] + continuousCols, outputCol="features") pipeline = Pipeline(stages=indexers + encoders + [assembler]) model=pipeline.fit(df) data = model.transform(df) data = data.withColumn('label',col(labelCol)) return data.select(indexCol,'features','label')Unsupervised learning version:
def get_dummy(df,indexCol,categoricalCols,continuousCols): ''' Get dummy variables and concat with continuous variables for unsupervised learning. :param df: the dataframe :param categoricalCols: the name list of the categorical data :param continuousCols: the name list of the numerical data :return k: feature matrix :author: Wenqiang Feng :email: von198@gmail.com ''' indexers = [ StringIndexer(inputCol=c, outputCol="{0}_indexed".format(c)) for c in categoricalCols ] # default setting: dropLast=True encoders = [ OneHotEncoder(inputCol=indexer.getOutputCol(), outputCol="{0}_encoded".format(indexer.getOutputCol())) for indexer in indexers ] assembler = VectorAssembler(inputCols=[encoder.getOutputCol() for encoder in encoders] + continuousCols, outputCol="features") pipeline = Pipeline(stages=indexers + encoders + [assembler]) model=pipeline.fit(df) data = model.transform(df) return data.select(indexCol,'features')
Two in one:
def get_dummy(df,indexCol,categoricalCols,continuousCols,labelCol,dropLast=False): ''' Get dummy variables and concat with continuous variables for ml modeling. :param df: the dataframe :param categoricalCols: the name list of the categorical data :param continuousCols: the name list of the numerical data :param labelCol: the name of label column :param dropLast: the flag of drop last column :return: feature matrix :author: Wenqiang Feng :email: von198@gmail.com >>> df = spark.createDataFrame([ (0, "a"), (1, "b"), (2, "c"), (3, "a"), (4, "a"), (5, "c") ], ["id", "category"]) >>> indexCol = 'id' >>> categoricalCols = ['category'] >>> continuousCols = [] >>> labelCol = [] >>> mat = get_dummy(df,indexCol,categoricalCols,continuousCols,labelCol) >>> mat.show() >>> +---+-------------+ | id| features| +---+-------------+ | 0|[1.0,0.0,0.0]| | 1|[0.0,0.0,1.0]| | 2|[0.0,1.0,0.0]| | 3|[1.0,0.0,0.0]| | 4|[1.0,0.0,0.0]| | 5|[0.0,1.0,0.0]| +---+-------------+ ''' from pyspark.ml import Pipeline from pyspark.ml.feature import StringIndexer, OneHotEncoder, VectorAssembler from pyspark.sql.functions import col indexers = [ StringIndexer(inputCol=c, outputCol="{0}_indexed".format(c)) for c in categoricalCols ] # default setting: dropLast=True encoders = [ OneHotEncoder(inputCol=indexer.getOutputCol(), outputCol="{0}_encoded".format(indexer.getOutputCol()),dropLast=dropLast) for indexer in indexers ] assembler = VectorAssembler(inputCols=[encoder.getOutputCol() for encoder in encoders] + continuousCols, outputCol="features") pipeline = Pipeline(stages=indexers + encoders + [assembler]) model=pipeline.fit(df) data = model.transform(df) if indexCol and labelCol: # for supervised learning data = data.withColumn('label',col(labelCol)) return data.select(indexCol,'features','label') elif not indexCol and labelCol: # for supervised learning data = data.withColumn('label',col(labelCol)) return data.select('features','label') elif indexCol and not labelCol: # for unsupervised learning return data.select(indexCol,'features') elif not indexCol and not labelCol: # for unsupervised learning return data.select('features')
from pyspark.sql import Row
from pyspark.ml.linalg import Vectors
# I provide two ways to build the features and labels
# method 1 (good for small feature):
#def transData(row):
# return Row(label=row["Sales"],
# features=Vectors.dense([row["TV"],
# row["Radio"],
# row["Newspaper"]]))
# Method 2 (good for large features):
def transData(data):
return data.rdd.map(lambda r: [Vectors.dense(r[:-1]),r[-1]]).toDF(['features','label'])
transformed= transData(df)
transformed.show(5)
+-----------------+-----+
| features|label|
+-----------------+-----+
|[230.1,37.8,69.2]| 22.1|
| [44.5,39.3,45.1]| 10.4|
| [17.2,45.9,69.3]| 9.3|
|[151.5,41.3,58.5]| 18.5|
|[180.8,10.8,58.4]| 12.9|
+-----------------+-----+
only showing top 5 rows
Note
You will find out that all of the machine learning algorithms in Spark are based on the features and label. That is to say, you can play with all of the machine learning algorithms in Spark when you get ready the features and label.
Convert the data to dense vector
# convert the data to dense vector
def transData(data):
return data.rdd.map(lambda r: [r[-1], Vectors.dense(r[:-1])]).\
toDF(['label','features'])
transformed = transData(df)
transformed.show(5)
Deal with the Categorical variables
from pyspark.ml import Pipeline
from pyspark.ml.regression import LinearRegression
from pyspark.ml.feature import VectorIndexer
from pyspark.ml.evaluation import RegressionEvaluator
# Automatically identify categorical features, and index them.
# We specify maxCategories so features with > 4
# distinct values are treated as continuous.
featureIndexer = VectorIndexer(inputCol="features", \
outputCol="indexedFeatures",\
maxCategories=4).fit(transformed)
data = featureIndexer.transform(transformed)
When you check you data at this point, you will get
+-----------------+-----+-----------------+
| features|label| indexedFeatures|
+-----------------+-----+-----------------+
|[230.1,37.8,69.2]| 22.1|[230.1,37.8,69.2]|
| [44.5,39.3,45.1]| 10.4| [44.5,39.3,45.1]|
| [17.2,45.9,69.3]| 9.3| [17.2,45.9,69.3]|
|[151.5,41.3,58.5]| 18.5|[151.5,41.3,58.5]|
|[180.8,10.8,58.4]| 12.9|[180.8,10.8,58.4]|
+-----------------+-----+-----------------+
only showing top 5 rows
Split the data into training and test sets (40% held out for testing)
# Split the data into training and test sets (40% held out for testing)
(trainingData, testData) = transformed.randomSplit([0.6, 0.4])
You can check your train and test data as follows (In my opinion, it is always to good to keep tracking your data during prototype pahse):
trainingData.show(5)
testData.show(5)
Then you will get
+---------------+-----+---------------+
| features|label|indexedFeatures|
+---------------+-----+---------------+
| [4.1,11.6,5.7]| 3.2| [4.1,11.6,5.7]|
|[7.3,28.1,41.4]| 5.5|[7.3,28.1,41.4]|
| [8.4,27.2,2.1]| 5.7| [8.4,27.2,2.1]|
| [8.6,2.1,1.0]| 4.8| [8.6,2.1,1.0]|
|[8.7,48.9,75.0]| 7.2|[8.7,48.9,75.0]|
+---------------+-----+---------------+
only showing top 5 rows
+----------------+-----+----------------+
| features|label| indexedFeatures|
+----------------+-----+----------------+
| [0.7,39.6,8.7]| 1.6| [0.7,39.6,8.7]|
| [5.4,29.9,9.4]| 5.3| [5.4,29.9,9.4]|
| [7.8,38.9,50.6]| 6.6| [7.8,38.9,50.6]|
|[17.2,45.9,69.3]| 9.3|[17.2,45.9,69.3]|
|[18.7,12.1,23.4]| 6.7|[18.7,12.1,23.4]|
+----------------+-----+----------------+
only showing top 5 rows
Fit Decision Tree Regression Model
from pyspark.ml.regression import DecisionTreeRegressor
# Train a DecisionTree model.
dt = DecisionTreeRegressor(featuresCol="indexedFeatures")
Pipeline Architecture
# Chain indexer and tree in a Pipeline
pipeline = Pipeline(stages=[featureIndexer, dt])
model = pipeline.fit(trainingData)
Make predictions
# Make predictions.
predictions = model.transform(testData)
# Select example rows to display.
predictions.select("features","label","predictedLabel").show(5)
+----------+-----+----------------+
|prediction|label| features|
+----------+-----+----------------+
| 7.2| 1.6| [0.7,39.6,8.7]|
| 7.3| 5.3| [5.4,29.9,9.4]|
| 7.2| 6.6| [7.8,38.9,50.6]|
| 8.64| 9.3|[17.2,45.9,69.3]|
| 6.45| 6.7|[18.7,12.1,23.4]|
+----------+-----+----------------+
only showing top 5 rows
Evaluation
from pyspark.ml.evaluation import RegressionEvaluator
from pyspark.ml.evaluation import RegressionEvaluator
# Select (prediction, true label) and compute test error
evaluator = RegressionEvaluator(labelCol="label",
predictionCol="prediction",
metricName="rmse")
rmse = evaluator.evaluate(predictions)
print("Root Mean Squared Error (RMSE) on test data = %g" % rmse)
The final Root Mean Squared Error (RMSE) is as follows:
Root Mean Squared Error (RMSE) on test data = 1.50999
y_true = predictions.select("label").toPandas()
y_pred = predictions.select("prediction").toPandas()
import sklearn.metrics
r2_score = sklearn.metrics.r2_score(y_true, y_pred)
print('r2_score: {0}'.format(r2_score))
Then you will get the 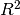 value:
value:
r2_score: 0.911024318967
You may also check the importance of the features:
model.stages[1].featureImportances
The you will get the weight for each features
SparseVector(3, {0: 0.6811, 1: 0.3187, 2: 0.0002})
9.4. Random Forest Regression¶
9.4.1. Introduction¶
9.4.2. How to solve it?¶
9.4.3. Demo¶
The Jupyter notebook can be download from Random Forest Regression.
For more details about the parameters, please visit Random Forest Regressor API .
Set up spark context and SparkSession
from pyspark.sql import SparkSession
spark = SparkSession \
.builder \
.appName("Python Spark RandomForest Regression example") \
.config("spark.some.config.option", "some-value") \
.getOrCreate()
Load dataset
df = spark.read.format('com.databricks.spark.csv').\
options(header='true', \
inferschema='true').\
load("../data/Advertising.csv",header=True);
df.show(5,True)
df.printSchema()
+-----+-----+---------+-----+
| TV|Radio|Newspaper|Sales|
+-----+-----+---------+-----+
|230.1| 37.8| 69.2| 22.1|
| 44.5| 39.3| 45.1| 10.4|
| 17.2| 45.9| 69.3| 9.3|
|151.5| 41.3| 58.5| 18.5|
|180.8| 10.8| 58.4| 12.9|
+-----+-----+---------+-----+
only showing top 5 rows
root
|-- TV: double (nullable = true)
|-- Radio: double (nullable = true)
|-- Newspaper: double (nullable = true)
|-- Sales: double (nullable = true)
df.describe().show()
+-------+-----------------+------------------+------------------+------------------+
|summary| TV| Radio| Newspaper| Sales|
+-------+-----------------+------------------+------------------+------------------+
| count| 200| 200| 200| 200|
| mean| 147.0425|23.264000000000024|30.553999999999995|14.022500000000003|
| stddev|85.85423631490805|14.846809176168728| 21.77862083852283| 5.217456565710477|
| min| 0.7| 0.0| 0.3| 1.6|
| max| 296.4| 49.6| 114.0| 27.0|
+-------+-----------------+------------------+------------------+------------------+
Convert the data to dense vector (features and label)
Note
You are strongly encouraged to try my
get_dummyfunction for dealing with the categorical data in comple dataset.Supervised learning version:
def get_dummy(df,indexCol,categoricalCols,continuousCols,labelCol): from pyspark.ml import Pipeline from pyspark.ml.feature import StringIndexer, OneHotEncoder, VectorAssembler from pyspark.sql.functions import col indexers = [ StringIndexer(inputCol=c, outputCol="{0}_indexed".format(c)) for c in categoricalCols ] # default setting: dropLast=True encoders = [ OneHotEncoder(inputCol=indexer.getOutputCol(), outputCol="{0}_encoded".format(indexer.getOutputCol())) for indexer in indexers ] assembler = VectorAssembler(inputCols=[encoder.getOutputCol() for encoder in encoders] + continuousCols, outputCol="features") pipeline = Pipeline(stages=indexers + encoders + [assembler]) model=pipeline.fit(df) data = model.transform(df) data = data.withColumn('label',col(labelCol)) return data.select(indexCol,'features','label')Unsupervised learning version:
def get_dummy(df,indexCol,categoricalCols,continuousCols): ''' Get dummy variables and concat with continuous variables for unsupervised learning. :param df: the dataframe :param categoricalCols: the name list of the categorical data :param continuousCols: the name list of the numerical data :return k: feature matrix :author: Wenqiang Feng :email: von198@gmail.com ''' indexers = [ StringIndexer(inputCol=c, outputCol="{0}_indexed".format(c)) for c in categoricalCols ] # default setting: dropLast=True encoders = [ OneHotEncoder(inputCol=indexer.getOutputCol(), outputCol="{0}_encoded".format(indexer.getOutputCol())) for indexer in indexers ] assembler = VectorAssembler(inputCols=[encoder.getOutputCol() for encoder in encoders] + continuousCols, outputCol="features") pipeline = Pipeline(stages=indexers + encoders + [assembler]) model=pipeline.fit(df) data = model.transform(df) return data.select(indexCol,'features')
Two in one:
def get_dummy(df,indexCol,categoricalCols,continuousCols,labelCol,dropLast=False): ''' Get dummy variables and concat with continuous variables for ml modeling. :param df: the dataframe :param categoricalCols: the name list of the categorical data :param continuousCols: the name list of the numerical data :param labelCol: the name of label column :param dropLast: the flag of drop last column :return: feature matrix :author: Wenqiang Feng :email: von198@gmail.com >>> df = spark.createDataFrame([ (0, "a"), (1, "b"), (2, "c"), (3, "a"), (4, "a"), (5, "c") ], ["id", "category"]) >>> indexCol = 'id' >>> categoricalCols = ['category'] >>> continuousCols = [] >>> labelCol = [] >>> mat = get_dummy(df,indexCol,categoricalCols,continuousCols,labelCol) >>> mat.show() >>> +---+-------------+ | id| features| +---+-------------+ | 0|[1.0,0.0,0.0]| | 1|[0.0,0.0,1.0]| | 2|[0.0,1.0,0.0]| | 3|[1.0,0.0,0.0]| | 4|[1.0,0.0,0.0]| | 5|[0.0,1.0,0.0]| +---+-------------+ ''' from pyspark.ml import Pipeline from pyspark.ml.feature import StringIndexer, OneHotEncoder, VectorAssembler from pyspark.sql.functions import col indexers = [ StringIndexer(inputCol=c, outputCol="{0}_indexed".format(c)) for c in categoricalCols ] # default setting: dropLast=True encoders = [ OneHotEncoder(inputCol=indexer.getOutputCol(), outputCol="{0}_encoded".format(indexer.getOutputCol()),dropLast=dropLast) for indexer in indexers ] assembler = VectorAssembler(inputCols=[encoder.getOutputCol() for encoder in encoders] + continuousCols, outputCol="features") pipeline = Pipeline(stages=indexers + encoders + [assembler]) model=pipeline.fit(df) data = model.transform(df) if indexCol and labelCol: # for supervised learning data = data.withColumn('label',col(labelCol)) return data.select(indexCol,'features','label') elif not indexCol and labelCol: # for supervised learning data = data.withColumn('label',col(labelCol)) return data.select('features','label') elif indexCol and not labelCol: # for unsupervised learning return data.select(indexCol,'features') elif not indexCol and not labelCol: # for unsupervised learning return data.select('features')
from pyspark.sql import Row
from pyspark.ml.linalg import Vectors
# convert the data to dense vector
#def transData(row):
# return Row(label=row["Sales"],
# features=Vectors.dense([row["TV"],
# row["Radio"],
# row["Newspaper"]]))
def transData(data):
return data.rdd.map(lambda r: [Vectors.dense(r[:-1]),r[-1]]).toDF(['features','label'])
Convert the data to dense vector
transformed= transData(df)
transformed.show(5)
+-----------------+-----+
| features|label|
+-----------------+-----+
|[230.1,37.8,69.2]| 22.1|
| [44.5,39.3,45.1]| 10.4|
| [17.2,45.9,69.3]| 9.3|
|[151.5,41.3,58.5]| 18.5|
|[180.8,10.8,58.4]| 12.9|
+-----------------+-----+
only showing top 5 rows
Deal with the Categorical variables
from pyspark.ml import Pipeline
from pyspark.ml.regression import LinearRegression
from pyspark.ml.feature import VectorIndexer
from pyspark.ml.evaluation import RegressionEvaluator
featureIndexer = VectorIndexer(inputCol="features", \
outputCol="indexedFeatures",\
maxCategories=4).fit(transformed)
data = featureIndexer.transform(transformed)
data.show(5,True)
+-----------------+-----+-----------------+
| features|label| indexedFeatures|
+-----------------+-----+-----------------+
|[230.1,37.8,69.2]| 22.1|[230.1,37.8,69.2]|
| [44.5,39.3,45.1]| 10.4| [44.5,39.3,45.1]|
| [17.2,45.9,69.3]| 9.3| [17.2,45.9,69.3]|
|[151.5,41.3,58.5]| 18.5|[151.5,41.3,58.5]|
|[180.8,10.8,58.4]| 12.9|[180.8,10.8,58.4]|
+-----------------+-----+-----------------+
only showing top 5 rows
Split the data into training and test sets (40% held out for testing)
# Split the data into training and test sets (40% held out for testing)
(trainingData, testData) = data.randomSplit([0.6, 0.4])
trainingData.show(5)
testData.show(5)
+----------------+-----+----------------+
| features|label| indexedFeatures|
+----------------+-----+----------------+
| [0.7,39.6,8.7]| 1.6| [0.7,39.6,8.7]|
| [8.6,2.1,1.0]| 4.8| [8.6,2.1,1.0]|
| [8.7,48.9,75.0]| 7.2| [8.7,48.9,75.0]|
|[11.7,36.9,45.2]| 7.3|[11.7,36.9,45.2]|
|[13.2,15.9,49.6]| 5.6|[13.2,15.9,49.6]|
+----------------+-----+----------------+
only showing top 5 rows
+---------------+-----+---------------+
| features|label|indexedFeatures|
+---------------+-----+---------------+
| [4.1,11.6,5.7]| 3.2| [4.1,11.6,5.7]|
| [5.4,29.9,9.4]| 5.3| [5.4,29.9,9.4]|
|[7.3,28.1,41.4]| 5.5|[7.3,28.1,41.4]|
|[7.8,38.9,50.6]| 6.6|[7.8,38.9,50.6]|
| [8.4,27.2,2.1]| 5.7| [8.4,27.2,2.1]|
+---------------+-----+---------------+
only showing top 5 rows
Fit RandomForest Regression Model
# Import LinearRegression class
from pyspark.ml.regression import RandomForestRegressor
# Define LinearRegression algorithm
rf = RandomForestRegressor() # featuresCol="indexedFeatures",numTrees=2, maxDepth=2, seed=42
Note
If you decide to use the indexedFeatures features, you need to add the parameter featuresCol="indexedFeatures".
Pipeline Architecture
# Chain indexer and tree in a Pipeline
pipeline = Pipeline(stages=[featureIndexer, rf])
model = pipeline.fit(trainingData)
Make predictions
predictions = model.transform(testData)
# Select example rows to display.
predictions.select("features","label", "prediction").show(5)
+---------------+-----+------------------+
| features|label| prediction|
+---------------+-----+------------------+
| [4.1,11.6,5.7]| 3.2| 8.155439814814816|
| [5.4,29.9,9.4]| 5.3|10.412769901394899|
|[7.3,28.1,41.4]| 5.5| 12.13735648148148|
|[7.8,38.9,50.6]| 6.6|11.321796703296704|
| [8.4,27.2,2.1]| 5.7|12.071421957671957|
+---------------+-----+------------------+
only showing top 5 rows
Evaluation
# Select (prediction, true label) and compute test error
evaluator = RegressionEvaluator(
labelCol="label", predictionCol="prediction", metricName="rmse")
rmse = evaluator.evaluate(predictions)
print("Root Mean Squared Error (RMSE) on test data = %g" % rmse)
Root Mean Squared Error (RMSE) on test data = 2.35912
import sklearn.metrics
r2_score = sklearn.metrics.r2_score(y_true, y_pred)
print('r2_score: {:4.3f}'.format(r2_score))
r2_score: 0.831
Feature importances
model.stages[-1].featureImportances
SparseVector(3, {0: 0.4994, 1: 0.3196, 2: 0.181})
model.stages[-1].trees
[DecisionTreeRegressionModel (uid=dtr_c75f1c75442c) of depth 5 with 43 nodes,
DecisionTreeRegressionModel (uid=dtr_70fc2d441581) of depth 5 with 45 nodes,
DecisionTreeRegressionModel (uid=dtr_bc8464f545a7) of depth 5 with 31 nodes,
DecisionTreeRegressionModel (uid=dtr_a8a7e5367154) of depth 5 with 59 nodes,
DecisionTreeRegressionModel (uid=dtr_3ea01314fcbc) of depth 5 with 47 nodes,
DecisionTreeRegressionModel (uid=dtr_be9a04ac22a6) of depth 5 with 45 nodes,
DecisionTreeRegressionModel (uid=dtr_38610d47328a) of depth 5 with 51 nodes,
DecisionTreeRegressionModel (uid=dtr_bf14aea0ad3b) of depth 5 with 49 nodes,
DecisionTreeRegressionModel (uid=dtr_cde24ebd6bb6) of depth 5 with 39 nodes,
DecisionTreeRegressionModel (uid=dtr_a1fc9bd4fbeb) of depth 5 with 57 nodes,
DecisionTreeRegressionModel (uid=dtr_37798d6db1ba) of depth 5 with 41 nodes,
DecisionTreeRegressionModel (uid=dtr_c078b73ada63) of depth 5 with 41 nodes,
DecisionTreeRegressionModel (uid=dtr_fd00e3a070ad) of depth 5 with 55 nodes,
DecisionTreeRegressionModel (uid=dtr_9d01d5fb8604) of depth 5 with 45 nodes,
DecisionTreeRegressionModel (uid=dtr_8bd8bdddf642) of depth 5 with 41 nodes,
DecisionTreeRegressionModel (uid=dtr_e53b7bae30f8) of depth 5 with 49 nodes,
DecisionTreeRegressionModel (uid=dtr_808a869db21c) of depth 5 with 47 nodes,
DecisionTreeRegressionModel (uid=dtr_64d0916bceb0) of depth 5 with 33 nodes,
DecisionTreeRegressionModel (uid=dtr_0891055fff94) of depth 5 with 55 nodes,
DecisionTreeRegressionModel (uid=dtr_19c8bbad26c2) of depth 5 with 51 nodes]
9.5. Gradient-boosted tree regression¶
9.5.1. Introduction¶
9.5.2. How to solve it?¶
9.5.3. Demo¶
The Jupyter notebook can be download from Gradient-boosted tree regression.
For more details about the parameters, please visit Gradient boosted tree API .
Set up spark context and SparkSession
from pyspark.sql import SparkSession
spark = SparkSession \
.builder \
.appName("Python Spark GBTRegressor example") \
.config("spark.some.config.option", "some-value") \
.getOrCreate()
Load dataset
df = spark.read.format('com.databricks.spark.csv').\
options(header='true', \
inferschema='true').\
load("../data/Advertising.csv",header=True);
df.show(5,True)
df.printSchema()
+-----+-----+---------+-----+
| TV|Radio|Newspaper|Sales|
+-----+-----+---------+-----+
|230.1| 37.8| 69.2| 22.1|
| 44.5| 39.3| 45.1| 10.4|
| 17.2| 45.9| 69.3| 9.3|
|151.5| 41.3| 58.5| 18.5|
|180.8| 10.8| 58.4| 12.9|
+-----+-----+---------+-----+
only showing top 5 rows
root
|-- TV: double (nullable = true)
|-- Radio: double (nullable = true)
|-- Newspaper: double (nullable = true)
|-- Sales: double (nullable = true)
df.describe().show()
+-------+-----------------+------------------+------------------+------------------+
|summary| TV| Radio| Newspaper| Sales|
+-------+-----------------+------------------+------------------+------------------+
| count| 200| 200| 200| 200|
| mean| 147.0425|23.264000000000024|30.553999999999995|14.022500000000003|
| stddev|85.85423631490805|14.846809176168728| 21.77862083852283| 5.217456565710477|
| min| 0.7| 0.0| 0.3| 1.6|
| max| 296.4| 49.6| 114.0| 27.0|
+-------+-----------------+------------------+------------------+------------------+
Convert the data to dense vector (features and label)
Note
You are strongly encouraged to try my
get_dummyfunction for dealing with the categorical data in comple dataset.Supervised learning version:
def get_dummy(df,indexCol,categoricalCols,continuousCols,labelCol): from pyspark.ml import Pipeline from pyspark.ml.feature import StringIndexer, OneHotEncoder, VectorAssembler from pyspark.sql.functions import col indexers = [ StringIndexer(inputCol=c, outputCol="{0}_indexed".format(c)) for c in categoricalCols ] # default setting: dropLast=True encoders = [ OneHotEncoder(inputCol=indexer.getOutputCol(), outputCol="{0}_encoded".format(indexer.getOutputCol())) for indexer in indexers ] assembler = VectorAssembler(inputCols=[encoder.getOutputCol() for encoder in encoders] + continuousCols, outputCol="features") pipeline = Pipeline(stages=indexers + encoders + [assembler]) model=pipeline.fit(df) data = model.transform(df) data = data.withColumn('label',col(labelCol)) return data.select(indexCol,'features','label')Unsupervised learning version:
def get_dummy(df,indexCol,categoricalCols,continuousCols): ''' Get dummy variables and concat with continuous variables for unsupervised learning. :param df: the dataframe :param categoricalCols: the name list of the categorical data :param continuousCols: the name list of the numerical data :return k: feature matrix :author: Wenqiang Feng :email: von198@gmail.com ''' indexers = [ StringIndexer(inputCol=c, outputCol="{0}_indexed".format(c)) for c in categoricalCols ] # default setting: dropLast=True encoders = [ OneHotEncoder(inputCol=indexer.getOutputCol(), outputCol="{0}_encoded".format(indexer.getOutputCol())) for indexer in indexers ] assembler = VectorAssembler(inputCols=[encoder.getOutputCol() for encoder in encoders] + continuousCols, outputCol="features") pipeline = Pipeline(stages=indexers + encoders + [assembler]) model=pipeline.fit(df) data = model.transform(df) return data.select(indexCol,'features')
Two in one:
def get_dummy(df,indexCol,categoricalCols,continuousCols,labelCol,dropLast=False): ''' Get dummy variables and concat with continuous variables for ml modeling. :param df: the dataframe :param categoricalCols: the name list of the categorical data :param continuousCols: the name list of the numerical data :param labelCol: the name of label column :param dropLast: the flag of drop last column :return: feature matrix :author: Wenqiang Feng :email: von198@gmail.com >>> df = spark.createDataFrame([ (0, "a"), (1, "b"), (2, "c"), (3, "a"), (4, "a"), (5, "c") ], ["id", "category"]) >>> indexCol = 'id' >>> categoricalCols = ['category'] >>> continuousCols = [] >>> labelCol = [] >>> mat = get_dummy(df,indexCol,categoricalCols,continuousCols,labelCol) >>> mat.show() >>> +---+-------------+ | id| features| +---+-------------+ | 0|[1.0,0.0,0.0]| | 1|[0.0,0.0,1.0]| | 2|[0.0,1.0,0.0]| | 3|[1.0,0.0,0.0]| | 4|[1.0,0.0,0.0]| | 5|[0.0,1.0,0.0]| +---+-------------+ ''' from pyspark.ml import Pipeline from pyspark.ml.feature import StringIndexer, OneHotEncoder, VectorAssembler from pyspark.sql.functions import col indexers = [ StringIndexer(inputCol=c, outputCol="{0}_indexed".format(c)) for c in categoricalCols ] # default setting: dropLast=True encoders = [ OneHotEncoder(inputCol=indexer.getOutputCol(), outputCol="{0}_encoded".format(indexer.getOutputCol()),dropLast=dropLast) for indexer in indexers ] assembler = VectorAssembler(inputCols=[encoder.getOutputCol() for encoder in encoders] + continuousCols, outputCol="features") pipeline = Pipeline(stages=indexers + encoders + [assembler]) model=pipeline.fit(df) data = model.transform(df) if indexCol and labelCol: # for supervised learning data = data.withColumn('label',col(labelCol)) return data.select(indexCol,'features','label') elif not indexCol and labelCol: # for supervised learning data = data.withColumn('label',col(labelCol)) return data.select('features','label') elif indexCol and not labelCol: # for unsupervised learning return data.select(indexCol,'features') elif not indexCol and not labelCol: # for unsupervised learning return data.select('features')
from pyspark.sql import Row
from pyspark.ml.linalg import Vectors
# convert the data to dense vector
#def transData(row):
# return Row(label=row["Sales"],
# features=Vectors.dense([row["TV"],
# row["Radio"],
# row["Newspaper"]]))
def transData(data):
return data.rdd.map(lambda r: [Vectors.dense(r[:-1]),r[-1]]).toDF(['features','label'])
Convert the data to dense vector
transformed= transData(df)
transformed.show(5)
+-----------------+-----+
| features|label|
+-----------------+-----+
|[230.1,37.8,69.2]| 22.1|
| [44.5,39.3,45.1]| 10.4|
| [17.2,45.9,69.3]| 9.3|
|[151.5,41.3,58.5]| 18.5|
|[180.8,10.8,58.4]| 12.9|
+-----------------+-----+
only showing top 5 rows
Deal with the Categorical variables
from pyspark.ml import Pipeline
from pyspark.ml.regression import GBTRegressor
from pyspark.ml.feature import VectorIndexer
from pyspark.ml.evaluation import RegressionEvaluator
featureIndexer = VectorIndexer(inputCol="features", \
outputCol="indexedFeatures",\
maxCategories=4).fit(transformed)
data = featureIndexer.transform(transformed)
data.show(5,True)
+-----------------+-----+-----------------+
| features|label| indexedFeatures|
+-----------------+-----+-----------------+
|[230.1,37.8,69.2]| 22.1|[230.1,37.8,69.2]|
| [44.5,39.3,45.1]| 10.4| [44.5,39.3,45.1]|
| [17.2,45.9,69.3]| 9.3| [17.2,45.9,69.3]|
|[151.5,41.3,58.5]| 18.5|[151.5,41.3,58.5]|
|[180.8,10.8,58.4]| 12.9|[180.8,10.8,58.4]|
+-----------------+-----+-----------------+
only showing top 5 rows
Split the data into training and test sets (40% held out for testing)
# Split the data into training and test sets (40% held out for testing)
(trainingData, testData) = data.randomSplit([0.6, 0.4])
trainingData.show(5)
testData.show(5)
+----------------+-----+----------------+
| features|label| indexedFeatures|
+----------------+-----+----------------+
| [0.7,39.6,8.7]| 1.6| [0.7,39.6,8.7]|
| [8.6,2.1,1.0]| 4.8| [8.6,2.1,1.0]|
| [8.7,48.9,75.0]| 7.2| [8.7,48.9,75.0]|
|[11.7,36.9,45.2]| 7.3|[11.7,36.9,45.2]|
|[13.2,15.9,49.6]| 5.6|[13.2,15.9,49.6]|
+----------------+-----+----------------+
only showing top 5 rows
+---------------+-----+---------------+
| features|label|indexedFeatures|
+---------------+-----+---------------+
| [4.1,11.6,5.7]| 3.2| [4.1,11.6,5.7]|
| [5.4,29.9,9.4]| 5.3| [5.4,29.9,9.4]|
|[7.3,28.1,41.4]| 5.5|[7.3,28.1,41.4]|
|[7.8,38.9,50.6]| 6.6|[7.8,38.9,50.6]|
| [8.4,27.2,2.1]| 5.7| [8.4,27.2,2.1]|
+---------------+-----+---------------+
only showing top 5 rows
Fit RandomForest Regression Model
# Import LinearRegression class
from pyspark.ml.regression import GBTRegressor
# Define LinearRegression algorithm
rf = GBTRegressor() #numTrees=2, maxDepth=2, seed=42
Note
If you decide to use the indexedFeatures features, you need to add the parameter featuresCol="indexedFeatures".
Pipeline Architecture
# Chain indexer and tree in a Pipeline
pipeline = Pipeline(stages=[featureIndexer, rf])
model = pipeline.fit(trainingData)
Make predictions
predictions = model.transform(testData)
# Select example rows to display.
predictions.select("features","label", "prediction").show(5)
+----------------+-----+------------------+
| features|label| prediction|
+----------------+-----+------------------+
| [7.8,38.9,50.6]| 6.6| 6.836040343319862|
| [8.6,2.1,1.0]| 4.8| 5.652202764688849|
| [8.7,48.9,75.0]| 7.2| 6.908750296855572|
| [13.1,0.4,25.6]| 5.3| 5.784020210692574|
|[19.6,20.1,17.0]| 7.6|6.8678921062629295|
+----------------+-----+------------------+
only showing top 5 rows
Evaluation
# Select (prediction, true label) and compute test error
evaluator = RegressionEvaluator(
labelCol="label", predictionCol="prediction", metricName="rmse")
rmse = evaluator.evaluate(predictions)
print("Root Mean Squared Error (RMSE) on test data = %g" % rmse)
Root Mean Squared Error (RMSE) on test data = 1.36939
import sklearn.metrics
r2_score = sklearn.metrics.r2_score(y_true, y_pred)
print('r2_score: {:4.3f}'.format(r2_score))
r2_score: 0.932
Feature importances
model.stages[-1].featureImportances
SparseVector(3, {0: 0.3716, 1: 0.3525, 2: 0.2759})
model.stages[-1].trees
[DecisionTreeRegressionModel (uid=dtr_7f5cd2ef7cb6) of depth 5 with 61 nodes,
DecisionTreeRegressionModel (uid=dtr_ef3ab6baeac9) of depth 5 with 39 nodes,
DecisionTreeRegressionModel (uid=dtr_07c6e3cf3819) of depth 5 with 45 nodes,
DecisionTreeRegressionModel (uid=dtr_ce724af79a2b) of depth 5 with 47 nodes,
DecisionTreeRegressionModel (uid=dtr_d149ecc71658) of depth 5 with 55 nodes,
DecisionTreeRegressionModel (uid=dtr_d3a79bdea516) of depth 5 with 43 nodes,
DecisionTreeRegressionModel (uid=dtr_7abc1a337844) of depth 5 with 51 nodes,
DecisionTreeRegressionModel (uid=dtr_480834b46d8f) of depth 5 with 33 nodes,
DecisionTreeRegressionModel (uid=dtr_0cbd1eaa3874) of depth 5 with 39 nodes,
DecisionTreeRegressionModel (uid=dtr_8088ac71a204) of depth 5 with 57 nodes,
DecisionTreeRegressionModel (uid=dtr_2ceb9e8deb45) of depth 5 with 47 nodes,
DecisionTreeRegressionModel (uid=dtr_cc334e84e9a2) of depth 5 with 57 nodes,
DecisionTreeRegressionModel (uid=dtr_a665c562929e) of depth 5 with 41 nodes,
DecisionTreeRegressionModel (uid=dtr_2999b1ffd2dc) of depth 5 with 45 nodes,
DecisionTreeRegressionModel (uid=dtr_29965cbe8cfc) of depth 5 with 55 nodes,
DecisionTreeRegressionModel (uid=dtr_731df51bf0ad) of depth 5 with 41 nodes,
DecisionTreeRegressionModel (uid=dtr_354cf33424da) of depth 5 with 51 nodes,
DecisionTreeRegressionModel (uid=dtr_4230f200b1c0) of depth 5 with 41 nodes,
DecisionTreeRegressionModel (uid=dtr_3279cdc1ce1d) of depth 5 with 45 nodes,
DecisionTreeRegressionModel (uid=dtr_f474a99ff06e) of depth 5 with 55 nodes]
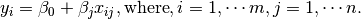
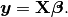
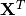 on side of
on side of 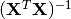 on both side of the former result. You may also apply the
on both side of the former result. You may also apply the