Homework #10

required library

library(plyr)

problem 24.12 a

Load data

dt <- read.table("./data/CH24PR12.txt", 
                col.names =  c("time", "gender", "sequence", "experience", "observation"))
dt[, 2] = as.factor(dt[,2])
dt[, 3] = as.factor(dt[,3])
dt[, 4] = as.factor(dt[,4])

residual for ANOVA model

fit = aov(time~gender+sequence+experience+gender*sequence+gender*experience+sequence*experience+gender*sequence*experience, data=dt)
residuals = cbind(dt, fit$residuals)
residuals

##    time gender sequence experience observation fit$residuals
## 1  1250      1        1          1           1          31.4
## 2  1175      1        1          1           2         -43.6
## 3  1236      1        1          1           3          17.4
## 4  1239      1        1          1           4          20.4
## 5  1193      1        1          1           5         -25.6
## 6  1021      1        1          2           1         -30.0
## 7  1099      1        1          2           2          48.0
## 8  1069      1        1          2           3          18.0
## 9   996      1        1          2           4         -55.0
## 10 1070      1        1          2           5          19.0
## 11 1319      1        2          1           1          44.8
## 12 1251      1        2          1           2         -23.2
## 13 1241      1        2          1           3         -33.2
## 14 1295      1        2          1           4          20.8
## 15 1265      1        2          1           5          -9.2
## 16 1119      1        2          2           1          -3.4
## 17 1110      1        2          2           2         -12.4
## 18 1123      1        2          2           3           0.6
## 19 1097      1        2          2           4         -25.4
## 20 1163      1        2          2           5          40.6
## 21 1217      1        3          1           1          -1.2
## 22 1190      1        3          1           2         -28.2
## 23 1201      1        3          1           3         -17.2
## 24 1232      1        3          1           4          13.8
## 25 1251      1        3          1           5          32.8
## 26 1033      1        3          2           1         -18.2
## 27 1067      1        3          2           2          15.8
## 28 1057      1        3          2           3           5.8
## 29 1077      1        3          2           4          25.8
## 30 1022      1        3          2           5         -29.2
## 31 1066      2        1          1           1          29.6
## 32 1076      2        1          1           2          39.6
## 33 1004      2        1          1           3         -32.4
## 34 1002      2        1          1           4         -34.4
## 35 1034      2        1          1           5          -2.4
## 36  864      2        1          2           1          -6.6
## 37  848      2        1          2           2         -22.6
## 38  881      2        1          2           3          10.4
## 39  892      2        1          2           4          21.4
## 40  868      2        1          2           5          -2.6
## 41 1105      2        2          1           1          27.6
## 42 1043      2        2          1           2         -34.4
## 43 1051      2        2          1           3         -26.4
## 44 1128      2        2          1           4          50.6
## 45 1060      2        2          1           5         -17.4
## 46  927      2        2          2           1          -4.6
## 47  944      2        2          2           2          12.4
## 48  957      2        2          2           3          25.4
## 49  897      2        2          2           4         -34.6
## 50  933      2        2          2           5           1.4
## 51 1021      2        3          1           1           0.6
## 52 1020      2        3          1           2          -0.4
## 53 1035      2        3          1           3          14.6
## 54 1000      2        3          1           4         -20.4
## 55 1026      2        3          1           5           5.6
## 56  841      2        3          2           1         -19.4
## 57  865      2        3          2           2           4.6
## 58  817      2        3          2           3         -43.4
## 59  911      2        3          2           4          50.6
## 60  868      2        3          2           5           7.6

Problem 24.12 b

Calculate correlation coefficient

res = lm(time~gender+sequence+experience+gender*sequence+gender*experience+sequence*experience+gender*sequence*experience, data=dt)
StdErr = summary(res)$sigma
n = length(res$residuals)
ExpVals = sapply(1:n, function(k) StdErr*qnorm((k-.375)/(n+.25)) )
r = cor(ExpVals, sort(res$residuals))
r

## [1] 0.9916214

problem 24.13 abcde

Problem 24.13 a

Calculate estimated treatment means

estimated_treatment_mean = ddply(dt, .(gender, sequence, experience), 
                                 summarize, mean = mean(time))
estimated_treatment_mean

##    gender sequence experience   mean
## 1       1        1          1 1218.6
## 2       1        1          2 1051.0
## 3       1        2          1 1274.2
## 4       1        2          2 1122.4
## 5       1        3          1 1218.2
## 6       1        3          2 1051.2
## 7       2        1          1 1036.4
## 8       2        1          2  870.6
## 9       2        2          1 1077.4
## 10      2        2          2  931.6
## 11      2        3          1 1020.4
## 12      2        3          2  860.4

AB plots

No interaction effects
Both gender and sequence have a main effect.

dat = dt[dt$experience == "1", ]
sequence = dat$sequence
gender = dat$gender
time = dat$time
interaction.plot(gender, sequence, time, main="Experience < 18 months")

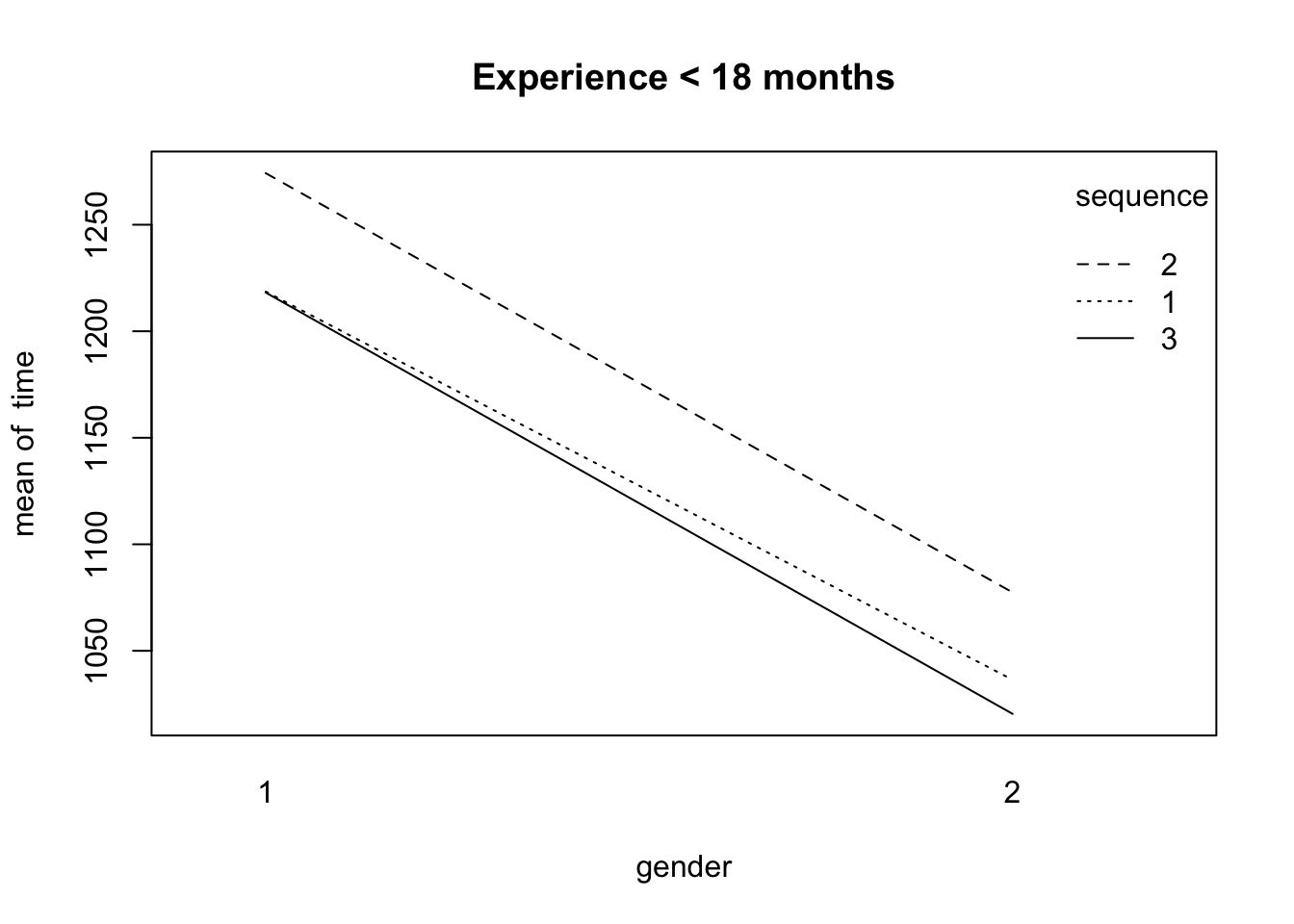
## experience level = 1
dat = dt[dt$experience == "2", ]
sequence = dat$sequence
gender = dat$gender
time = dat$time
interaction.plot(gender, sequence, time, main="Experience > 18 months")

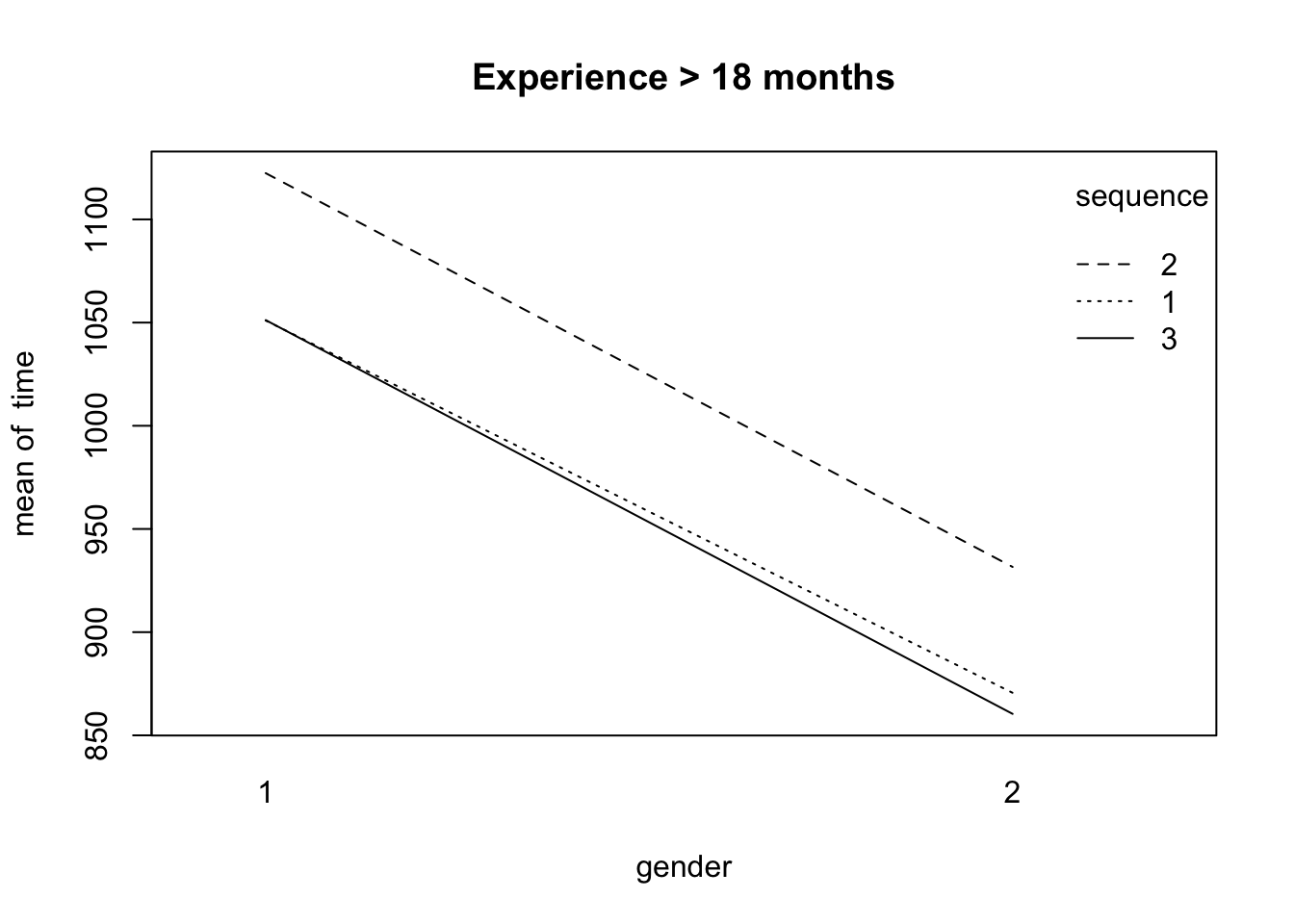
Problem 24.13 b

fit = aov(time~gender+sequence+experience+gender*sequence+gender*experience+
            sequence*experience+gender*sequence*experience, data=dt)
variance_table = summary(fit)
variance_table = round(as.matrix(variance_table[[1]]), 3)
variance_table[,1:3]

##                            Df     Sum Sq    Mean Sq
## gender                      1 540360.600 540360.600
## sequence                    2  49319.633  24659.817
## experience                  1 382401.667 382401.667
## gender:sequence             2    542.500    271.250
## gender:experience           1     91.267     91.267
## sequence:experience         2    911.233    455.617
## gender:sequence:experience  2     19.033      9.517
## Residuals                  48  41186.000    858.042

Problem 24.13 c

Test for three-factor interactions

alternatives
- H0: all $(\alpha\beta\gamma){ijk}$ equal zero
- Ha: not all $(\alpha\beta\gamma){ijk}$ equal zero
decision rules: if $F^*$ ≤ F(1-0.05; 2, 48), conclude H0; otherwise, conclude Ha.
conclusion: $F^*$ =0.011 < F(1-0.05; 2, 48) = 0.531, conclude H0.
pvalue = 0.989

variance_table[7,, drop=F]

##                            Df Sum Sq Mean Sq F value Pr(>F)
## gender:sequence:experience  2 19.033   9.517   0.011  0.989

Problem 24.13 d

Test for AB, AC, BC interactions

AB interaction

alternatives
- H0: all $(\alpha\beta)_{ij}$ equal zero
- Ha: not all $(\alpha\beta)_{ij}$ equal zero
decision rules: if $F^*$ ≤ F(1-0.05; 2, 48), conclude H0; otherwise, conclude Ha.
conclusion: $F^*$ = 0.316 < F(1-0.05; 2, 48) = 3.190727, conclude H0.
pvalue = 0.730

qf(0.95,2,48)

## [1] 3.190727

variance_table[4,, drop=F]

##                            Df Sum Sq Mean Sq F value Pr(>F)
## gender:sequence             2  542.5  271.25   0.316   0.73

AC interaction

alternatives
- H0: all $(\alpha\gamma)_{ik}$ equal zero
- Ha: not all (αγ)ik equal zero
decision rules: if $F^*$ ≤ F(1-0.05; 1, 48), conclude H0; otherwise, conclude Ha.
conclusion: $F^*$ = 0.106 < F(1-0.05; 1, 48) = 4.042652, conclude H0.
pvalue = 0.746

qf(0.95,1,48)

## [1] 4.042652

variance_table[5,, drop=F]

##                            Df Sum Sq Mean Sq F value Pr(>F)
## gender:experience           1 91.267  91.267   0.106  0.746

BC interaction

alternatives
- H0: all $(\beta\gamma)_{jk}$ equal zero
- Ha: not all $(\beta\gamma)_{jk}$ equal zero
decision rules: if $F^*$ ≤ F(1-0.05; 2, 48), conclude H0; otherwise, conclude Ha.
conclusion: $F^*$ = 0.106 < F(1-0.05; 2, 48) = 0.531, conclude H0.
pvalue = 0.591

qf(0.95,2,48)

## [1] 3.190727

variance_table[6,, drop=F]

##                            Df  Sum Sq Mean Sq F value Pr(>F)
## sequence:experience         2 911.233 455.617   0.531  0.591

Problem 24.13 e

Test for main effects

main effect from A

alternatives
- H0: all $\alpha_i$ (i=1,2) equal zero
- Ha: not all $$\alpha_i$ $ equal zero
decision rules: if $F^*$ ≤ F(1-0.05; 1, 48), conclude H0; otherwise, conclude Ha.
conclusion: $F^*$ = 629.76 > F(1-0.05; 1, 48) =4.042652, conclude Ha.
pvalue = 0

qf(0.95,1,48)

## [1] 4.042652

variance_table[1,, drop=F]

##                            Df   Sum Sq  Mean Sq F value Pr(>F)
## gender                      1 540360.6 540360.6  629.76      0

main effect from B

alternatives
- H0: all $\beta_j$ (j=1,2,3) equal zero
- Ha: not all $\beta_j$ equal zero
decision rules: if $F^*$ ≤ F(1-0.05; 2, 48), conclude H0; otherwise, conclude Ha.
conclusion: $F^*$ = 28.74 > F(1-0.05; 2, 48) = 3.190727, conclude Ha.
pvalue = 0

qf(0.95,2,48)

## [1] 3.190727

variance_table[2,, drop=F]

##                            Df   Sum Sq  Mean Sq F value Pr(>F)
## sequence                    2 49319.63 24659.82   28.74      0

main effect from C

alternatives
- H0: all $\gamma_k$ (k=1,2) equal zero
- Ha: not all $\gamma_k$ equal zero
decision rules: if $F^*$ ≤ F(1-0.05; 1, 48), conclude H0; otherwise, conclude Ha.
conclusion: $F^*$ = 445.668 > F(1-0.05; 1, 48) = 4.042652, conclude Ha.
pvalue = 0

qf(0.95,1,48)

## [1] 4.042652

variance_table[3,, drop=F]

##                            Df   Sum Sq  Mean Sq F value Pr(>F)
## experience                  1 382401.7 382401.7 445.668      0

Problem 24.14 a

D1 = 189.8

D = ddply(dt, .(gender), summarize, mean = mean(time))
D1 = D[1,2] - D[2,2]
D1

## [1] 189.8

D2 = -57.25

D = ddply(dt, .(sequence), summarize, mean = mean(time))
D2 = D[1,2] - D[2,2]
D2

## [1] -57.25

D3 = 6.6

D = ddply(dt, .(sequence), summarize, mean = mean(time))
D3 = D[1,2] - D[3,2]
D3

## [1] 6.6

D4 = 63.85

D = ddply(dt, .(sequence), summarize, mean = mean(time))
D4 = D[2,2] - D[3,2]
D4

## [1] 63.85

D5 = 159.6667

D = ddply(dt, .(experience), summarize, mean = mean(time))
D5 = D[1,2] - D[2,2]
D5

## [1] 159.6667

MSE = 858.042

MSE = variance_table[8,3,drop=F]
MSE

##                            Mean Sq
## Residuals                  858.042

a = 2
b = 3
c = 2
n = 5
s{D1} = ((MSE/(nbc))[1^2 + (-1)^2])^0.5 = 7.563253
s{D2} = s{D3} = s{D4} = ((MSE/(nac))[1^2 + (-1)^2])^0.5 = 9.263056
s{D5} = ((MSE/(nab))[1^2 + (-1)^2])^0.5 = 7.563253
B = t[1-a/2g; (n-1)*abc] = t(1-0.1/(2*5); 48) = t(0.99; 48) = 2.406581
confidence coefficients
- D1 = [171.5984, 208.0016]
- D2 = [-79.54229, -34.95771]
- D3 = [-15.69229, 28.89229]
- D4 = [41.55771, 86.14229]
- D5 = [141.4651, 177.8683]
findings: D1, D2, D4, D5 are significant, but D3 is not significant.

Problem 24.14 b

Y231 = 1020.4

Y = ddply(dt, .(gender, sequence, experience), summarize, mean = mean(time))
Y213 = Y[11,]
Y213

##    gender sequence experience   mean
## 11      2        3          1 1020.4

s{Y231} = (MSE/n)^0.5 = 13.09994
t(1-0.05/2; 48) = 2.010635
confidence interval = [Y - t(1-0.05/2; 48)*s{Y231}, Y + t(1-0.05/2; 48)*s{Y231}]
confidence interval = [994.0608, 1046.739]

Homework #10

Wenqiang Feng

3/6/2017

required library

problem 24.12 a

Problem 24.12 b

problem 24.13 abcde

Problem 24.13 a

Calculate estimated treatment means

AB plots

Problem 24.13 b

Problem 24.13 c

Test for three-factor interactions

Problem 24.13 d

Test for AB, AC, BC interactions

AB interaction

AC interaction

BC interaction

Problem 24.13 e

Test for main effects

main effect from A

main effect from B

main effect from C

Problem 24.14 a

Problem 24.14 b